Ký hiệu S,p lần lượt là diện tích và nửa chu vi của tam giác ABC.
\(r=r_a-r_b-r_c\)
\(\Leftrightarrow\dfrac{S}{p}=\dfrac{S}{p-a}-\dfrac{S}{p-b}-\dfrac{S}{p-c}\)
\(\Leftrightarrow\dfrac{1}{a+b+c}=\dfrac{1}{b+c-a}-\dfrac{1}{c+a-b}-\dfrac{1}{a+b-c}\)
\(\Leftrightarrow\dfrac{1}{c+a-b}+\dfrac{1}{a+b-c}=\dfrac{1}{b+c-a}-\dfrac{1}{a+b+c}\)
\(\Leftrightarrow\dfrac{2a}{\left(c+a-b\right)\left(a+b-c\right)}=\dfrac{2a}{\left(b+c-a\right)\left(a+b+c\right)}\)
\(\Leftrightarrow a^2-\left(b-c\right)^2=\left(b+c\right)^2-a^2\)
\(\Leftrightarrow a^2=b^2+c^2\) hay tam giác ABC vuông tại A.
Vậy ta có điều phải chứng minh.

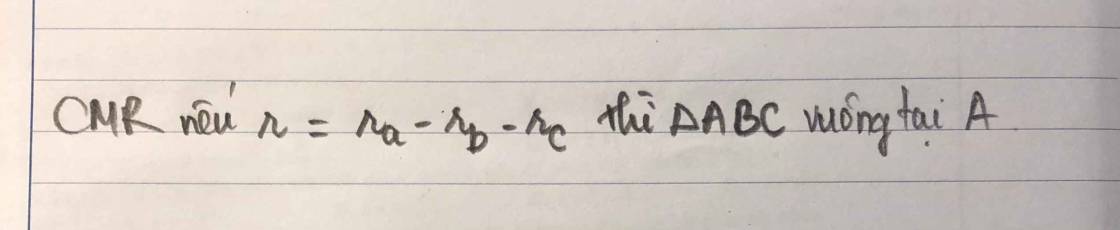














 ai giúp em với ạ :<< em đang cần gấp lắm, giải hộ em 2 bài thì càng tốt ạ, em xin chân thành cám ơn
ai giúp em với ạ :<< em đang cần gấp lắm, giải hộ em 2 bài thì càng tốt ạ, em xin chân thành cám ơn