6: \(-3x^2+4x-9\)
\(=-3\left(x^2-\dfrac{4}{3}x+3\right)\)
\(=-3\left(x^2-2\cdot x\cdot\dfrac{2}{3}+\dfrac{4}{9}+\dfrac{23}{9}\right)\)
\(=-3\left(x-\dfrac{2}{3}\right)^2-\dfrac{23}{3}< =-\dfrac{23}{3}< 0\forall x\)(ĐPCM)
7: \(x^2-2\sqrt{11}x+11\)
\(=x^2-2\cdot x\cdot\sqrt{11}+\left(\sqrt{11}\right)^2\)
\(=\left(x-\sqrt{11}\right)^2>=0\forall x\)(ĐPCM)
8: \(-5x^2+2x-7\)
\(=-5\left(x^2-\dfrac{2}{5}x+\dfrac{7}{5}\right)\)
\(=-5\left(x^2-2\cdot x\cdot\dfrac{1}{5}+\dfrac{1}{25}+\dfrac{34}{25}\right)\)
\(=-5\left(x-\dfrac{1}{5}\right)^2-\dfrac{34}{5}< =-\dfrac{34}{5}< 0\forall x\left(ĐPCM\right)\)
9: \(2x^2-4x+9\)
\(=2\left(x^2-2x+\dfrac{9}{2}\right)\)
\(=2\left(x^2-2x+1+\dfrac{7}{2}\right)\)
\(=2\left(x-1\right)^2+7>=7>0\forall x\)
10: \(-3x^2+4x-13\)
\(=-3\left(x^2-\dfrac{4}{3}x+\dfrac{13}{3}\right)\)
\(=-3\left(x^2-2\cdot x\cdot\dfrac{2}{3}+\dfrac{4}{9}+\dfrac{35}{9}\right)\)
\(=-3\left(x-\dfrac{2}{3}\right)^2-\dfrac{35}{3}< =-\dfrac{35}{3}< 0\forall x\)
11: \(-x^2+2x-3\)
\(=-\left(x^2-2x+3\right)\)
\(=-\left(x^2-2x+1+2\right)\)
\(=-\left(x-1\right)^2-2< =-2< 0\forall x\left(ĐPCM\right)\)
12: \(5x^2-4x+10\)
\(=5\left(x^2-\dfrac{4}{5}x+2\right)\)
\(=5\left(x^2-2\cdot x\cdot\dfrac{2}{5}+\dfrac{4}{25}+\dfrac{46}{25}\right)\)
\(=5\left(x-\dfrac{2}{5}\right)^2+\dfrac{46}{5}>=\dfrac{46}{5}>0\forall x\)
13: \(x^2-2x\sqrt{7}+7>=0\)
=>\(\left(x-\sqrt{7}\right)^2>=0\)(luôn đúng)
=>ĐPCM
14: \(3x^2+2x+5\)
\(=3\left(x^2+\dfrac{2}{3}x+\dfrac{5}{3}\right)\)
\(=3\left(x^2+2\cdot x\cdot\dfrac{1}{3}+\dfrac{1}{9}+\dfrac{14}{9}\right)\)
\(=3\left(x+\dfrac{1}{3}\right)^2+\dfrac{14}{3}>=\dfrac{14}{3}>0\forall x\left(ĐPCM\right)\)
15:
\(-3x^2-2x-10\)
\(=-3\left(x^2+\dfrac{2}{3}x+\dfrac{10}{3}\right)\)
\(=-3\left(x^2+2\cdot x\cdot\dfrac{1}{3}+\dfrac{1}{9}+\dfrac{29}{9}\right)\)
\(=-3\left(x+\dfrac{1}{3}\right)^2-\dfrac{29}{3}< =-\dfrac{29}{3}< 0\forall x\)(ĐPCM)

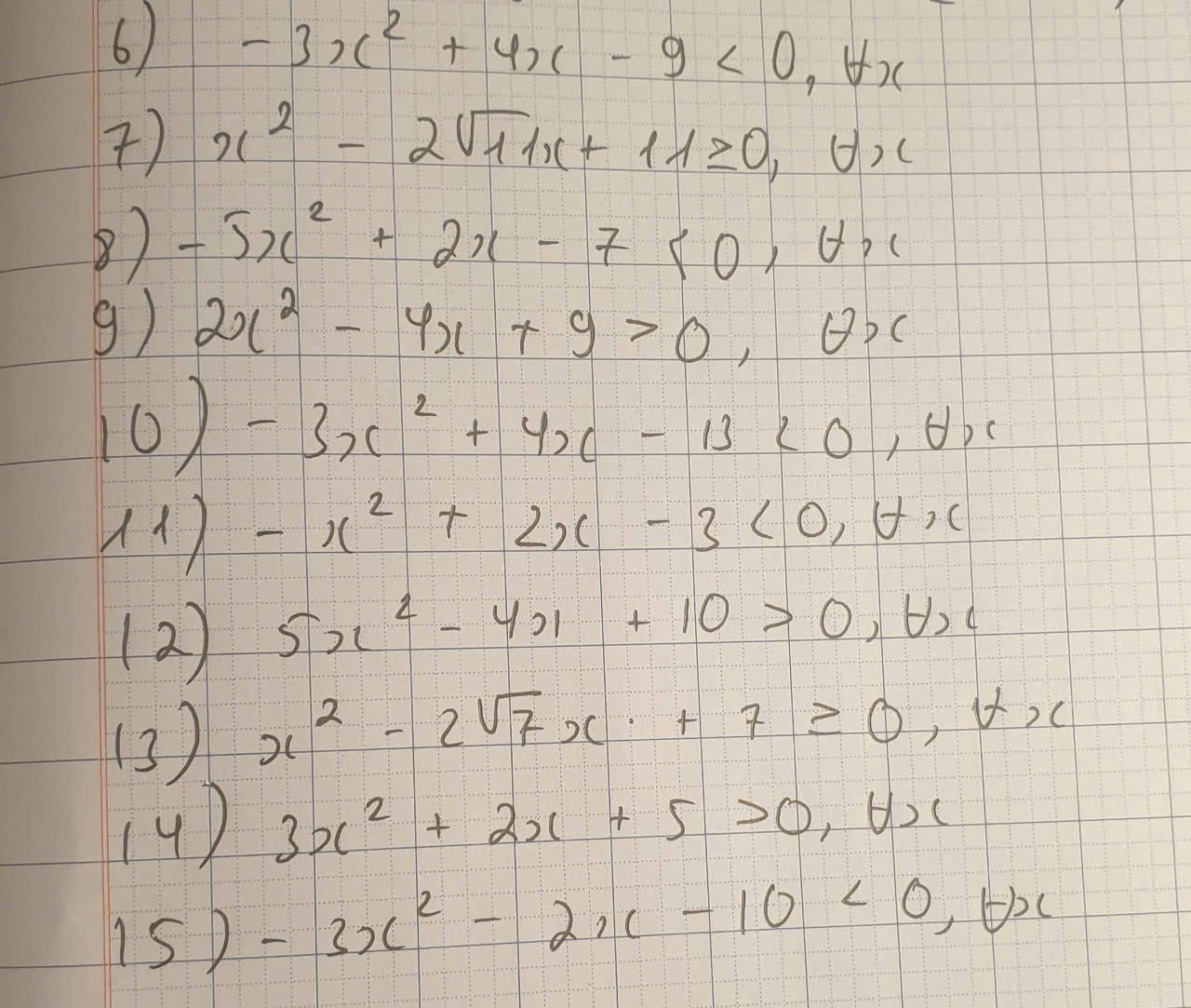 giải giúp mình với ạ
giải giúp mình với ạ