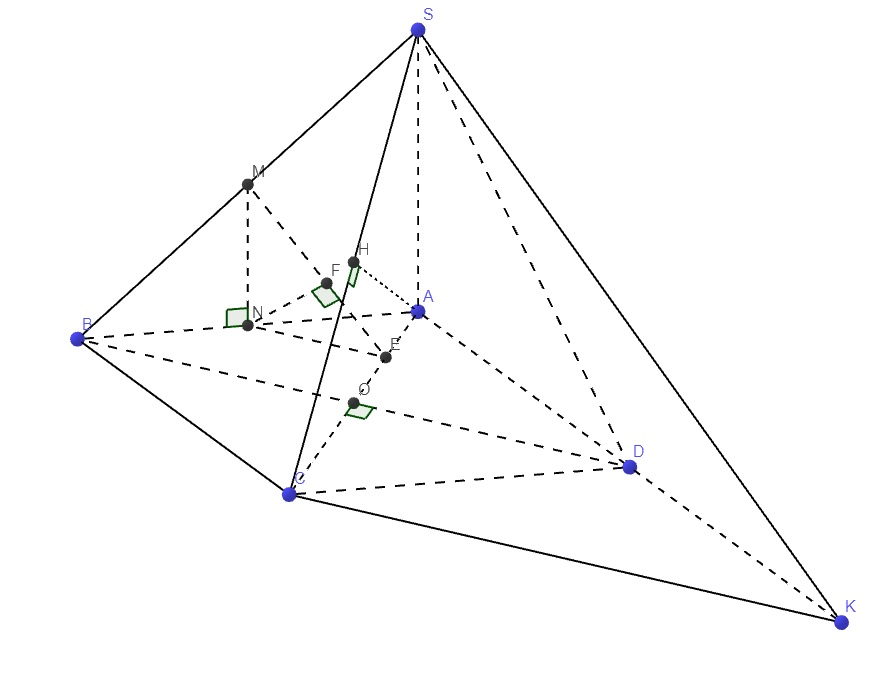
a.
Gọi O là giao điểm AC và BD
\(\widehat{BAC}=\widehat{DAC}=\dfrac{1}{2}\widehat{BAD}=60^0\Rightarrow\) các tam giác ABC, ABD đều
\(\Rightarrow AC=2a\) ; \(OB=OD=\dfrac{2a.\sqrt{3}}{2}=a\sqrt{3}\) (trung tuyến tam giác đều)
\(\Rightarrow BD=OB+OD=2a\sqrt{3}\)
\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABCD)
\(\Rightarrow\widehat{SCA}=45^0\Rightarrow SA=AC.tan\widehat{SCA}=2a\)
\(V=\dfrac{1}{3}SA.\dfrac{1}{2}AC.BD=\dfrac{4a^3\sqrt{3}}{3}\)
b.
Ý tưởng giải quyết khi gặp những câu này: đưa về tính k/c từ "chân đường vuông góc đến mặt phẳng". Ví dụ ở đây chân đường vuông góc với mặt (ABCD) là A. Nhưng A thuộc (AMC) nên ko sử dụng được, vậy cần tạo ra chân đường vuông góc mới bằng cách tạo ra 1 đường vuông góc mới. Do SA vuông góc đáy nên đường mới sẽ song song SA, và đường này cần cắt (AMC). Vậy chắc chắn nó đi qua M. Kết luận: ta chỉ cần tạo ra 1 đường thẳng đi qua M và song song SA là xong vấn đề. Sau đó chỉ cần dựa trên tỉ lệ khoảng cách là tính được.
Qua M kẻ đường thẳng song song SA cắt AB tại N \(\Rightarrow MN\) là đường trung bình tam giác SAB (đi qua trung điểm M cạnh bên và song song cạnh đáy SA) \(\Rightarrow MN\perp\left(ABCD\right)\Rightarrow MN\perp AC\) (1) và N là trung điểm AB
Đồng thời \(MN=\dfrac{1}{2}SA=a\)
\(\left\{{}\begin{matrix}BD\cap\left(AMC\right)=O\\OB=OD\end{matrix}\right.\) \(\Rightarrow d\left(D;\left(AMC\right)\right)=d\left(B;\left(AMC\right)\right)\)
\(\left\{{}\begin{matrix}BN\cap\left(AMC\right)=A\\BA=2NA\end{matrix}\right.\) \(\Rightarrow d\left(B;\left(AMC\right)\right)=2d\left(N;\left(AMC\right)\right)\)
\(\Rightarrow d\left(D;\left(AMC\right)\right)=2d\left(N;\left(AMC\right)\right)\)
Trong mp (ABCD), từ N kẻ \(NE\perp AC\left(2\right)\Rightarrow NE\) là đường trung bình tam giác ABO
\(\Rightarrow NE=\dfrac{1}{2}OB=\dfrac{a\sqrt{3}}{2}\)
Trong mp (MNE), từ N kẻ \(NF\perp ME\) (3)
\(\left(1\right);\left(2\right)\Rightarrow AC\perp\left(MNE\right)\Rightarrow AC\perp NF\) (4)
(3);(4) \(\Rightarrow NF\perp\left(AMC\right)\Rightarrow NF=d\left(N;\left(AMC\right)\right)\)
Hệ thức lượng: \(NF=\dfrac{MN.NE}{\sqrt{MN^2+NE^2}}=\dfrac{a\sqrt{21}}{7}\)
\(\Rightarrow d\left(D;\left(AMC\right)\right)=2NF=\dfrac{2a\sqrt{21}}{7}\)
c.
K đối xứng A qua D nên D là trung điểm AK
Theo giả thiết O là trung điểm AC (t/c hình thoi)
\(\Rightarrow OD\) là đường trung bình tam giác ACK
\(\Rightarrow OD||CK\) hay \(BD||CK\)
\(\Rightarrow BD||\left(SCK\right)\Rightarrow d\left(BD;SK\right)=d\left(BD;\left(SCK\right)\right)=d\left(O;\left(SCK\right)\right)\) (do O thuộc BD)
Lại có \(\left\{{}\begin{matrix}AO\cap\left(SCK\right)=C\\AC=2OC\end{matrix}\right.\) \(\Rightarrow d\left(A;\left(SCK\right)\right)=2d\left(O;\left(SCK\right)\right)\)
\(\Rightarrow d\left(BD;SK\right)=\dfrac{1}{2}d\left(A;\left(SCK\right)\right)\) (đưa được về chân đường vuông góc là A)
Từ A kẻ \(AH\perp SC\) (H thuộc SC) (5)
\(SA\perp\left(ABCD\right)\Rightarrow SA\perp CK\)
\(\left\{{}\begin{matrix}CK||BD\left(cmt\right)\\BD\perp AC\end{matrix}\right.\) \(\Rightarrow CK\perp AC\)
\(\Rightarrow CK\perp\left(SAC\right)\) \(\Rightarrow CK\perp AH\) (6)
(5);(6) \(\Rightarrow AH\perp\left(SCK\right)\Rightarrow AH=d\left(A;\left(SCK\right)\right)\)
Hệ thức lượng: \(AH=\dfrac{SA.AC}{\sqrt{SA^2+AC^2}}=a\sqrt{2}\)
\(\Rightarrow d\left(BD;SK\right)=\dfrac{1}{2}AH=\dfrac{a\sqrt{2}}{2}\)

 giải giúp mình câu 3 với, trọng tâm ở câu B và câu C, khó quá tôi không thể tìm ra hướng đi
giải giúp mình câu 3 với, trọng tâm ở câu B và câu C, khó quá tôi không thể tìm ra hướng đi