Gọi 3 số đó là n, n+1 và n+2
Theo bài ra ta có:
\(\Leftrightarrow n\left(n+1\right)\left(n+2\right)-\left(n+1\right)^3=15\)
\(\Leftrightarrow n^3+3n^2+2n-\left(n^3+3n^2+3n+1\right)=15\)
\(\Leftrightarrow-n-1=15\)
\(\Leftrightarrow n=-16\)
Vậy 3 số đó là \(-16;-15;-14\)
Gọi ba số cần tìm lần lượt là n;n+1;n+2
Theo đề, ta có phương trình:
\(n\left(n+1\right)\left(n+2\right)-\left(n+1\right)^3=15\)
\(\Leftrightarrow n^3+3n^2+2n-n^3-3n^2-3n-1=15\)
\(\Leftrightarrow-n=16\)
hay n=-16
Vậy: Ba số cần tìm là -16;-15;-14










 CÁC BẠN GIÚP MÌNH NHÉ MÌNH CẢM ƠN
CÁC BẠN GIÚP MÌNH NHÉ MÌNH CẢM ƠN






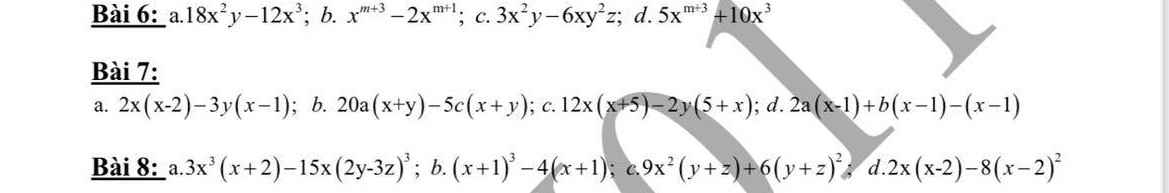 giúp mình nhanh với mình sắp học rồi.Camon các bạn rất nhìu :>>
giúp mình nhanh với mình sắp học rồi.Camon các bạn rất nhìu :>>