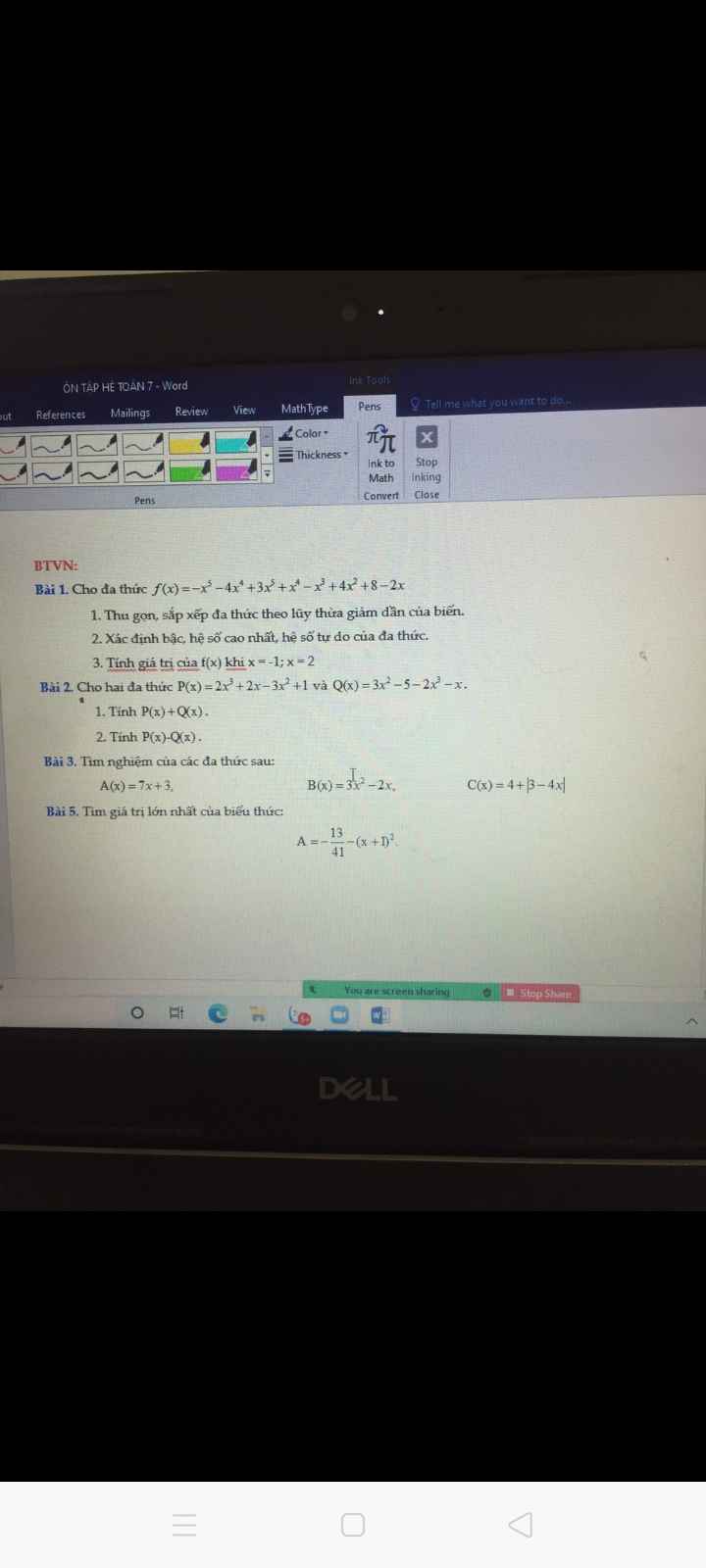
a) Ta có: \(\widehat{MPD}=\dfrac{\widehat{MPN}}{2}\)(PD là tia phân giác của \(\widehat{MPN}\))
\(\widehat{MNA}=\dfrac{\widehat{MNP}}{2}\)(NA là tia phân giác của \(\widehat{MNP}\))
mà \(\widehat{MPN}=\widehat{MNP}\)(ΔMNP vuông cân tại M)
nên \(\widehat{MPD}=\widehat{MNA}\)
Xét ΔMNA vuông tại M và ΔMPD vuông tại M có
MN=MP(ΔMNP vuông cân tại M)
\(\widehat{MPD}=\widehat{MNA}\)(cmt)
Do đó: ΔMNA=ΔMPD(Cạnh góc vuông-góc nhọn kề)
Suy ra: MA=MD(Hai cạnh tương ứng)
hay DN=AP(đpcm)