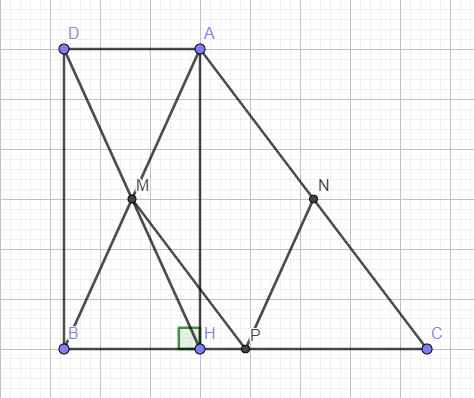
cho tam giác abc có ba góc nhọn (AB<AC) gọi ah là đường cao và M, N, P lần lượt là trung điểm AB,AC và BC. Gọi d là đối xứng của h qua m
a)c/m tứ giác DAHB là hcn
b) tìm đk của tam giác của ABC để AMPN là hcn
Đề nè mng:<<
a.
Ta có D đối xứng H qua M \(\Rightarrow M\) là trung điểm DH
Mà M là trung điểm AB theo giả thiết
\(\Rightarrow\) Tứ giác DAHB là hình bình hành (hai đường chéo cắt nhau tại trung điểm mỗi đường)
Lại có \(AH\perp BC\) (gt) \(\Rightarrow\widehat{AHB}=90^0\)
\(\Rightarrow\) DAHB là hình chữ nhật (hbh có 1 góc vuông)
b.
N là trung điểm AC, P là trung điểm BC \(\Rightarrow\left\{{}\begin{matrix}NP=\dfrac{1}{2}AB\\NP||AB\end{matrix}\right.\)
M là trung điểm AB \(\Rightarrow AM=\dfrac{1}{2}AB\) \(\Rightarrow\left\{{}\begin{matrix}NP=AM\\NP||AM\end{matrix}\right.\)
\(\Rightarrow\) Tứ giác AMPN là hình bình hành (cặp cạnh đối song song và bằng nhau)
Để AMPN là hình chữ nhật \(\Rightarrow\widehat{BAC}=90^0\)
\(\Rightarrow\) Tam giác ABC là tam giác vuông tại A