Bài 2:
a: \(P=\dfrac{x^4+x^3+x+1}{x^4-x^3+2x^2-x+1}\)
\(=\dfrac{x^3\left(x+1\right)+\left(x+1\right)}{x^4-x^3+x^2+x^2-x+1}\)
\(=\dfrac{\left(x+1\right)\left(x^3+1\right)}{x^2\left(x^2-x+1\right)+\left(x^2-x+1\right)}=\dfrac{\left(x+1\right)^2\cdot\left(x^2-x+1\right)}{\left(x^2-x+1\right)\left(x^2+1\right)}=\dfrac{\left(x+1\right)^2}{x^2+1}\)
\(\left(x+1\right)^2>=0\forall x\)
\(x^2+1>=1>0\forall x\)
Do đó: \(P=\dfrac{\left(x+1\right)^2}{x^2+1}>=0\forall x\)
=>P không âm với mọi x
b: ĐKXĐ: \(x\notin\left\{-2;-3;-4;-5;-6\right\}\)
\(\dfrac{1}{x^2+5x+6}+\dfrac{1}{x^2+7x+12}+\dfrac{1}{x^2+9x+20}+\dfrac{1}{x^2+11x+30}=\dfrac{1}{8}\)
=>\(\dfrac{1}{\left(x+2\right)\left(x+3\right)}+\dfrac{1}{\left(x+3\right)\left(x+4\right)}+\dfrac{1}{\left(x+4\right)\left(x+5\right)}+\dfrac{1}{\left(x+5\right)\left(x+6\right)}=\dfrac{1}{8}\)
=>\(\dfrac{1}{x+2}-\dfrac{1}{x+3}+\dfrac{1}{x+3}-...+\dfrac{1}{x+5}-\dfrac{1}{x+6}=\dfrac{1}{8}\)
=>\(\dfrac{1}{x+2}-\dfrac{1}{x+6}=\dfrac{1}{8}\)
=>\(\dfrac{x+6-x-2}{x^2+8x+12}=\dfrac{1}{8}\)
=>\(x^2+8x+12=8\cdot4=32\)
=>\(x^2+8x-20=0\)
=>(x+10)(x-2)=0
=>\(\left[{}\begin{matrix}x=-10\\x=2\end{matrix}\right.\)
Bài 5:
\(a+1>=2\sqrt{a};b+1>=2\sqrt{b};c+1>=2\sqrt{c}\)
Do đó: \(\left(a+1\right)\left(b+1\right)\left(c+1\right)>=2\sqrt{a}\cdot2\sqrt{b}\cdot2\sqrt{c}=8\sqrt{abc}=8\)

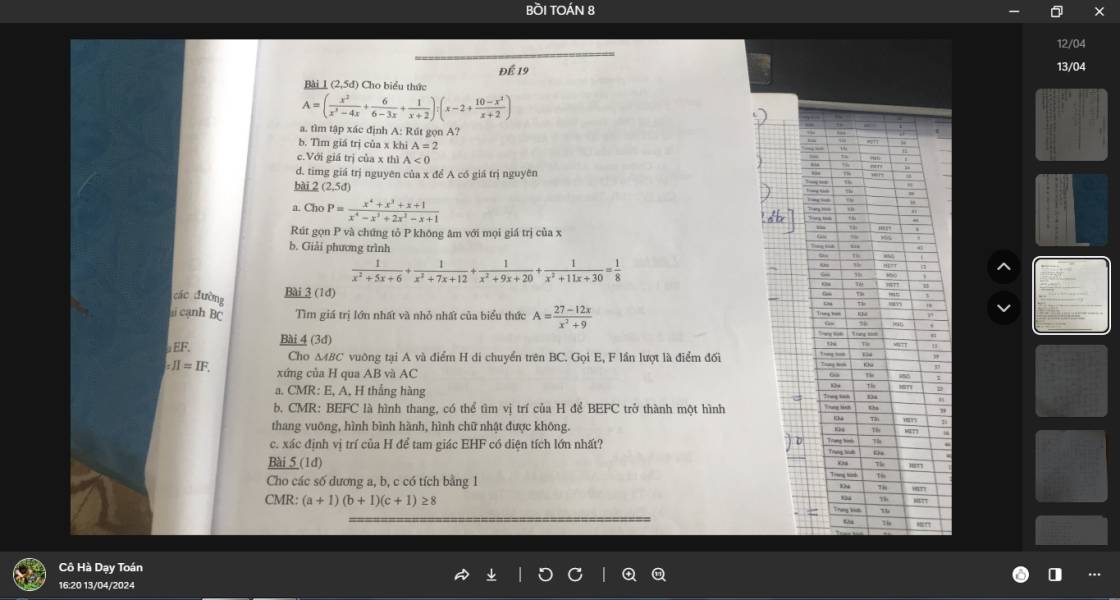




 ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ
ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn
ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn