Câu 1: Gọi số lập được có dạng là \(\overline{abcd}\)
a có 4 cách chọn
b có 4 cách chọn
c có 3 cách chọn
d có 2 cách chọn
Do đó: Có \(4\cdot4\cdot3\cdot2=16\cdot6=96\left(cách\right)\)
Câu 2:
a: Gọi số lập được có dạng là \(\overline{abcdef}\)
TH1: f=0
a có 9 cách chọn
b có 8 cách chọn
c có 7 cách chọn
d có 6 cách chọn
e có 5 cách chọn
Do đó: Có \(9\cdot8\cdot7\cdot6\cdot5=15120\left(cách\right)\)
TH2: f=5
a có 8 cách chọn
b có 8 cách chọn
c có 7 cách chọn
d có 6 cách chọn
e có 5 cách chọn
Do đó: Có \(8\cdot8\cdot7\cdot6\cdot5=13440\left(cách\right)\)
Tổng số cách là:
15120+13440=28560(cách)
b: Gọi số lập được có dạng là \(\overline{abc}\)
TH1: c=0
a có 9 cách chọn
b có 8 cách chọn
Do đó: Có \(9\cdot8=72\left(cách\right)\)
TH2: \(c\ne0\)
c có 4 cách chọn(2;4;6;8)
a có 8 cách chọn
b có 8 cách chọn
Do đó: Có \(8\cdot8\cdot4=64\cdot4=256\left(cách\right)\)
Tổng số cách là 256+72=328(cách)












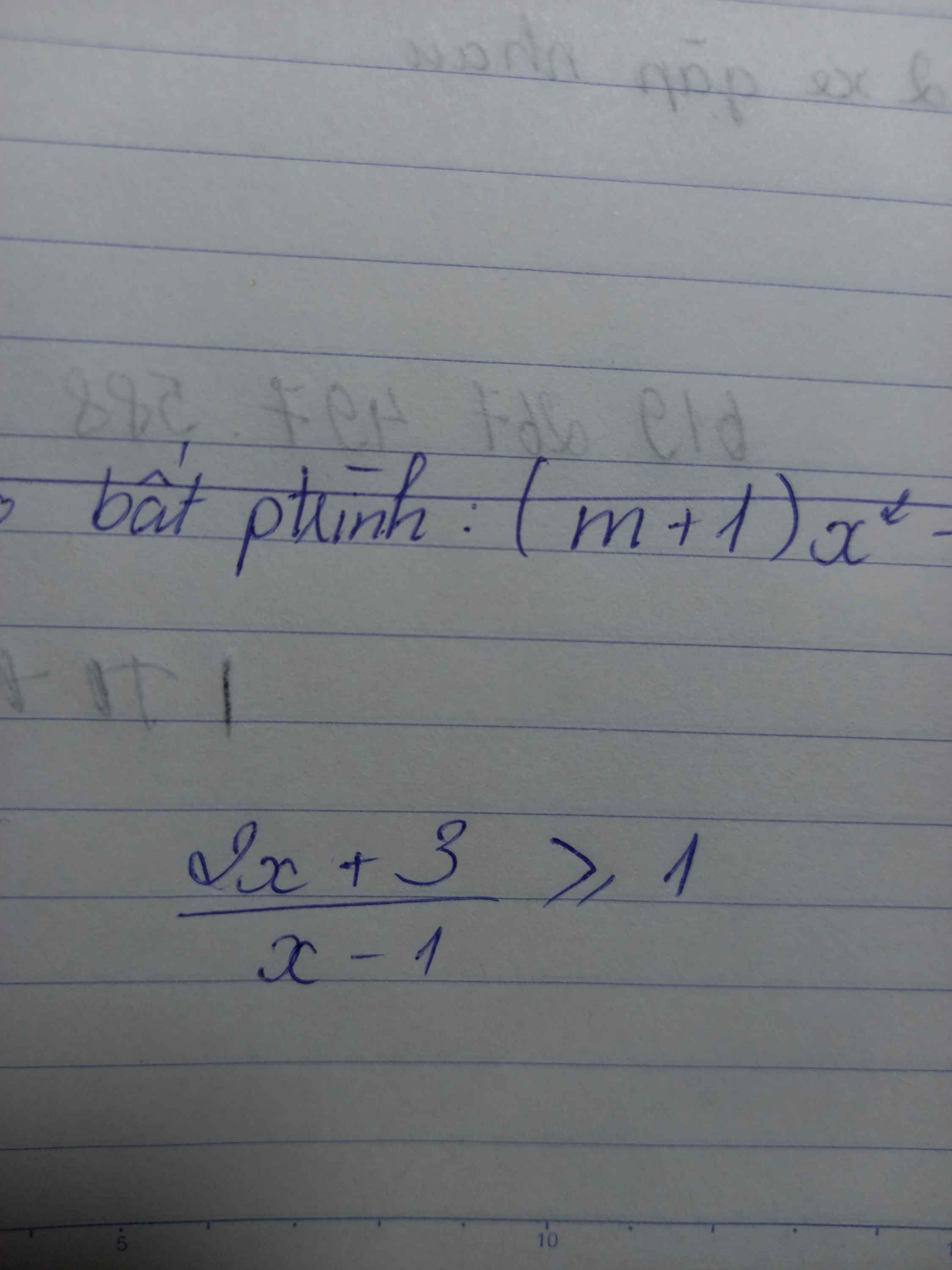






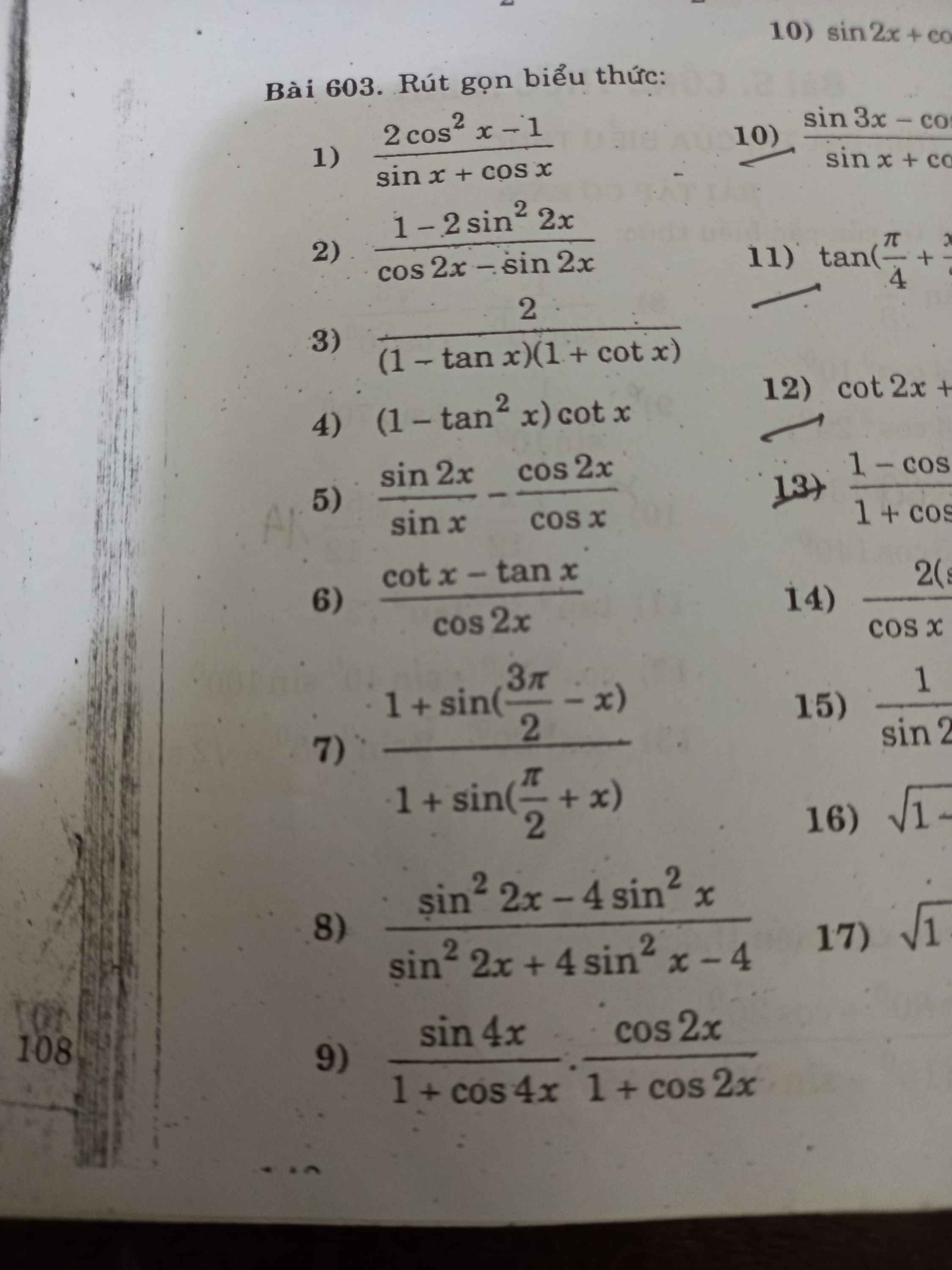

 ai giúp em với ạ :<< em đang cần gấp lắm, giải hộ em 2 bài thì càng tốt ạ, em xin chân thành cám ơn
ai giúp em với ạ :<< em đang cần gấp lắm, giải hộ em 2 bài thì càng tốt ạ, em xin chân thành cám ơn