\(P=\left(\dfrac{2x+1}{x\sqrt{x}+1}-\dfrac{\sqrt{x}}{x-\sqrt{x}+1}\right)\cdot\left(x-\dfrac{x-4}{\sqrt{x}-2}\right)\)
\(=\left(\dfrac{2x+1}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}-\dfrac{\sqrt{x}}{x-\sqrt{x}+1}\right)\cdot\left(x-\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}{\sqrt{x}-2}\right)\)
\(=\dfrac{2x+1-\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}\cdot\left[x-\left(\sqrt{x}+2\right)\right]\)
\(=\dfrac{x-\sqrt{x}+1}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}\cdot\left(x-\sqrt{x}-2\right)\)
\(=\dfrac{x-\sqrt{x}-2}{\sqrt{x}+1}=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\sqrt{x}+1}=\sqrt{x}-2\)

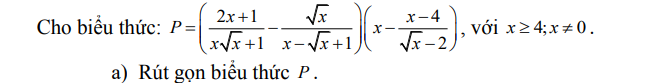




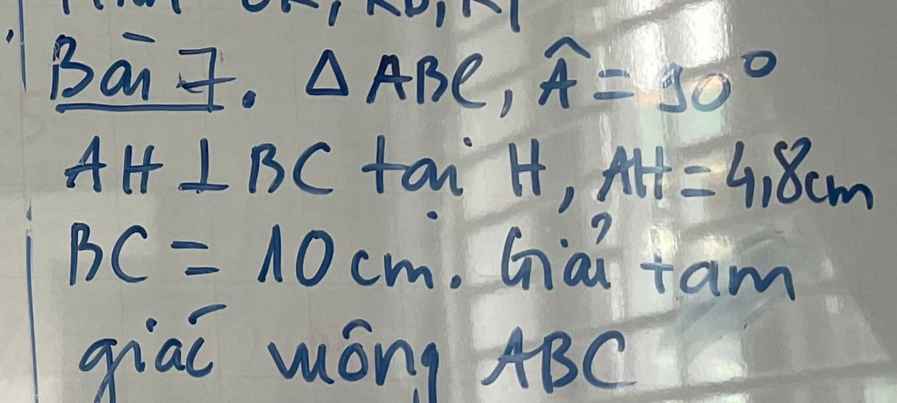













 em cần giải gấp bài 2 ạ, mọi người giúp em với ạ
em cần giải gấp bài 2 ạ, mọi người giúp em với ạ


