2:
a: Thay x=-1 vào (P), ta được:
\(y=2\cdot\left(-1\right)^2=2\)
Vậy: A(-1;2)
Thay x=2 vào (P), ta được:
\(y=2\cdot2^2=8\)
vậy:B(2;8)
A(-1;2); B(2;8)
Gọi (d): y=ax+b(a<>0) là phương trình đường thẳng AB
Thay x=-1 và y=2 vào (d), ta được:
\(a\cdot\left(-1\right)+b=2\)
=>-a+b=2(1)
Thay x=2 và y=8 vào (d), ta được:
\(2\cdot a+b=8\left(2\right)\)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}-a+b=2\\2a+b=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3a=-6\\a-b=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=2\\b=a+2=2+2=4\end{matrix}\right.\)
Vậy: (AB): y=2x+4
b: Để A,B,C thẳng hàng thì
Thay x=2m+1 và \(y=2m^2\) vào y=2x+4, ta được:
\(2m^2=2\left(2m+1\right)+4\)
=>\(m^2=2m+1+2\)
=>\(m^2-2m-3=0\)
=>(m-3)(m+1)=0
=>\(\left[{}\begin{matrix}m-3=0\\m+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=3\\m=-1\end{matrix}\right.\)
1:
a: Khi m=-2 thì phương trình sẽ trở thành:
\(x^2+2x+\left(-2\right)-1=0\)
=>\(x^2+2x-3=0\)
=>(x+3)(x-1)=0
=>\(\left[{}\begin{matrix}x+3=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=1\end{matrix}\right.\)
b: \(\text{Δ}=2^2-4\left(m-1\right)\)
=4-4m+4=-4m+8
Để phương trình có hai nghiệm thì Δ>=0
=>-4m+8>=0
=>-4m>=-8
=>\(m< =\dfrac{-8}{-4}=2\)
Theo Vi-et, ta có: \(\left\{{}\begin{matrix}x_1+x_2=-2\\x_1\cdot x_2=m-1\end{matrix}\right.\)
mà \(x_1+2x_2=1\)
nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}x_1+x_2=-2\\x_1+2x_2=1\\x_1\cdot x_2=m-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-x_2=-3\\x_1+x_2=-3\\x_1\cdot x_2=m-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x_2=3\\x_1=-3-x_2=-6\\x_1\cdot x_2=m-1\end{matrix}\right.\)
=>\(m-1=3\cdot\left(-6\right)=-18\)
=>m=-18+1=-17

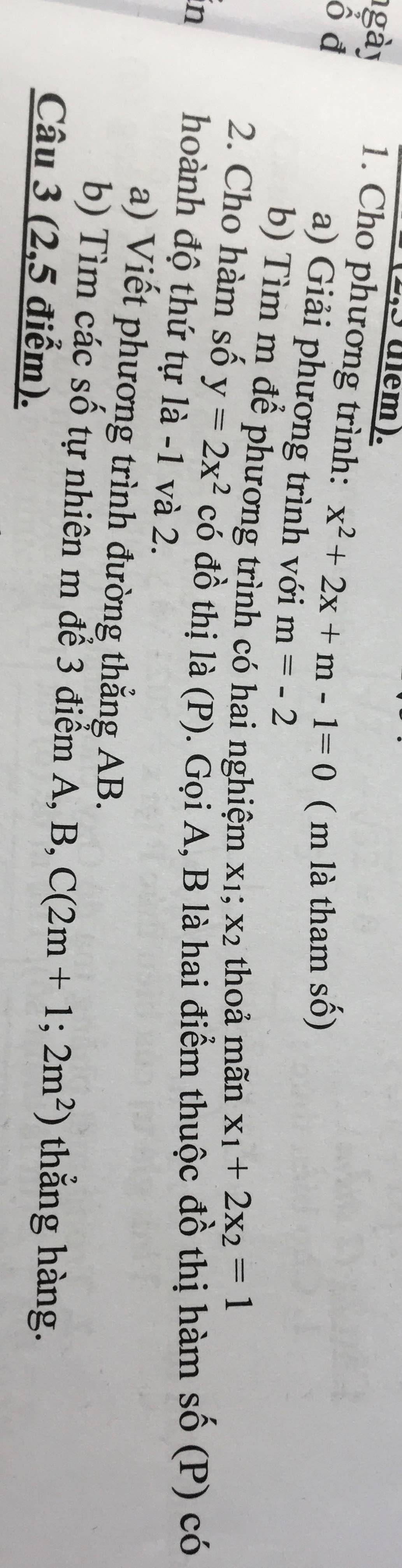

















 em cần giải gấp bài 2 ạ, mọi người giúp em với ạ
em cần giải gấp bài 2 ạ, mọi người giúp em với ạ


