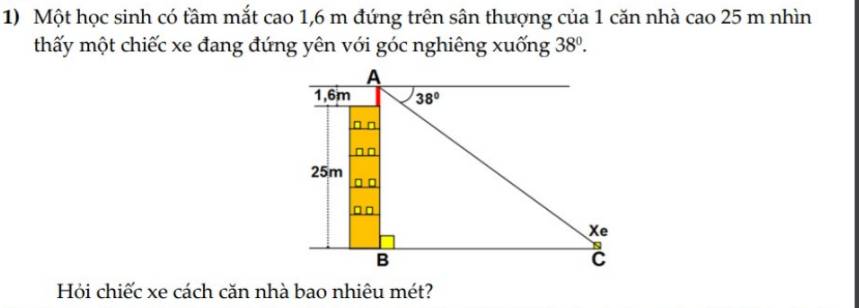
1: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB và OM là phân giác của góc AOB
Xét (O') có
MA,MC là các tiếp tuyến
Do đó: MA=MC và O'M là phân giác của góc AO'C
Ta có: MA=MB
MA=MC
Do đó: MB=MC
=>M là trung điểm của BC
Xét ΔABC có
AM là đường trung tuyến
\(AM=\dfrac{BC}{2}\)
Do đó: ΔABC vuông tại A
=>\(\widehat{BAC}=90^0\)
2: Ta có: OB\(\perp\)BC
O'C\(\perp\)BC
Do đó: OB//O'C
=>\(\widehat{BOA}+\widehat{CO'A}=180^0\)
=>\(2\cdot\left(\widehat{MOA}+\widehat{MO'A}\right)=180^0\)
=>\(\widehat{MOA}+\widehat{MO'A}=90^0\)
=>ΔMO'O vuông tại M
Xét ΔMO'O vuông tại M có MA là đường cao
nên \(MA^2=OA\cdot O'A\)
=>\(MA^2=R\cdot R'\)
=>\(MA=\sqrt{R\cdot R'}\)
=>\(BC=2\cdot MA=2\cdot\sqrt{R\cdot R'}\)
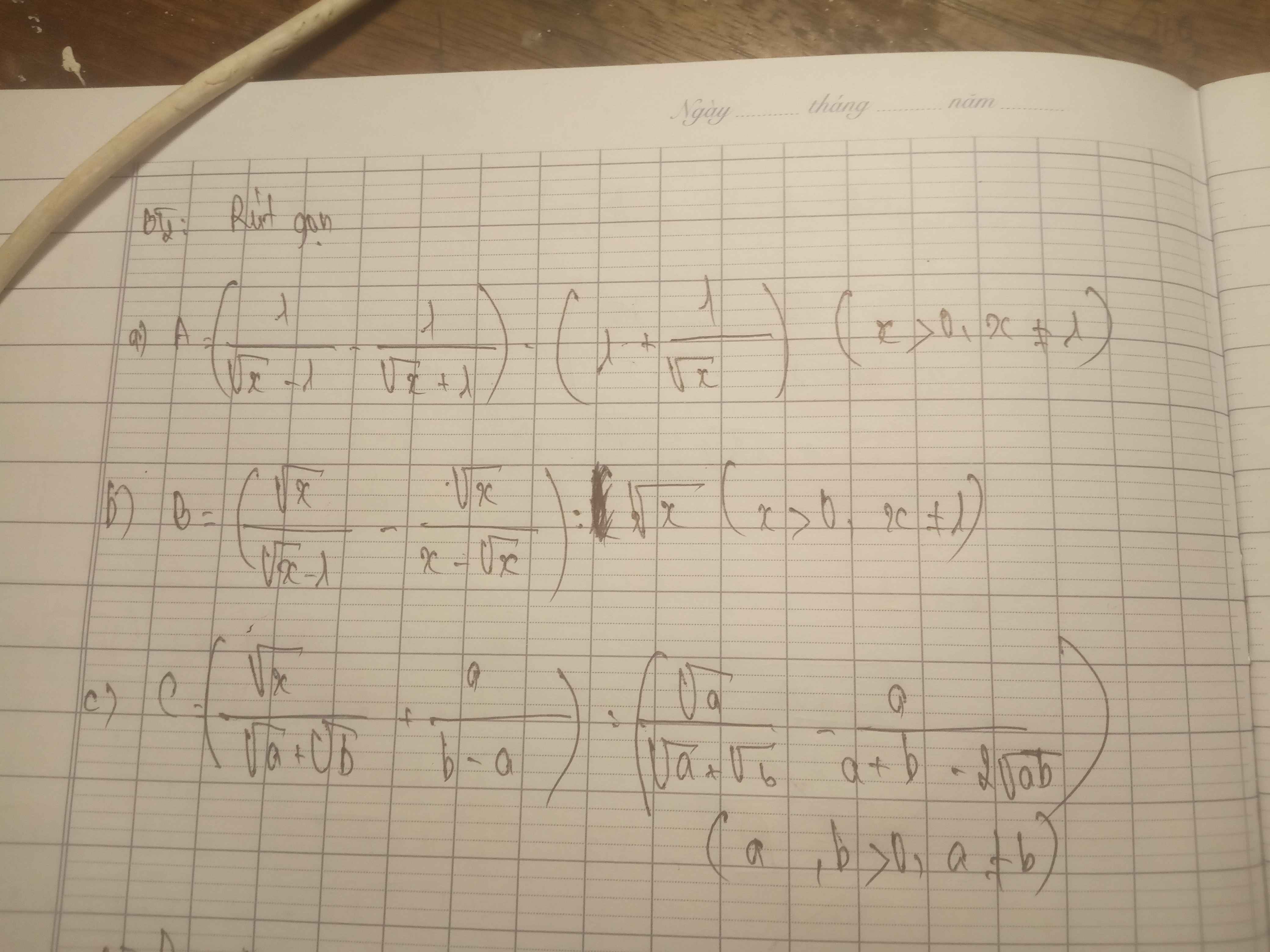
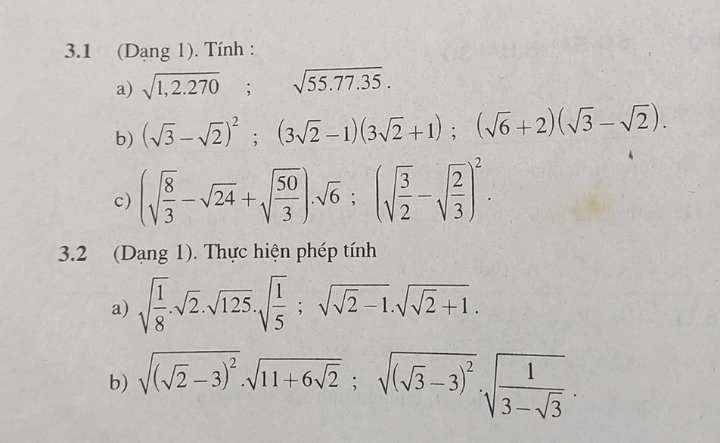
giúp em giải chi tiết với ạ
