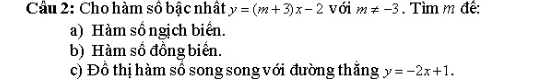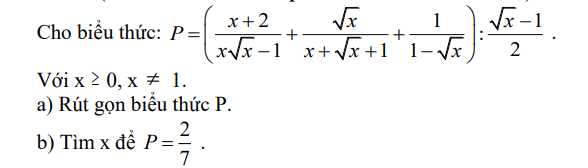a, Với \(x\ge0,x\ne1\)
\(P=\dfrac{2}{x+\sqrt{x}+1}\)
b, Với \(x\ge0,x\ne1\)
Để \(P=\dfrac{2}{7}\Leftrightarrow\dfrac{2}{x+\sqrt{x}+1}=\dfrac{2}{7}\)
\(\Rightarrow x+\sqrt{x}+1=7\)
\(\Leftrightarrow x+\sqrt{x}-6=0\)
\(\Leftrightarrow x-2\sqrt{x}+3\sqrt{x}-6=0\)
\(\Leftrightarrow\sqrt{x}.\left(\sqrt{x}-2\right)+3.\left(\sqrt{x}-2\right)=0\)
\(\Leftrightarrow\left(\sqrt{x}+3\right).\left(\sqrt{x}-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=-3\left(l,do\sqrt{x}\ge0\right)\\\sqrt{x}=2\end{matrix}\right.\)\(\Leftrightarrow x=4\) (t/m)
Vậy x = 4 thì 'P = 2/7'
Đúng 1
Bình luận (0)
Các câu hỏi tương tự
Dạ giải giúp em với ạ mai em phải nộp rồi ạ
Nếu được thì giải hộ em câu b,c thôi cũng được ạ
Giải giúp em câu b ạ

Giải giúp em câu b với ạ

Giải giúp em câu a,b,c với ạ !
Giải giúp em bài 8 ( câu b ) vs ạ
Giúp em câu A với câu C giải nhanh giúp em ạ 
 mng giải giúp em câu 10 với ạ, em cảm ơn ạ!
mng giải giúp em câu 10 với ạ, em cảm ơn ạ!
 mng giải giúp em câu 15 với ạ, em cảm ơn ạ!
mng giải giúp em câu 15 với ạ, em cảm ơn ạ!
Giúp em câu 11 với ạ, bài này em chưa học tới nên k biết làm thế nào; ; giải thích giúp em nhé. Em camon ạ^^
giải giúp em câu này ạ