ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)
ΔABC vuông tại A
mà AI là đường trung tuyến
nên \(AI=\dfrac{BC}{2}=\dfrac{5}{2}=2,5\left(cm\right)\)
a: Gọi M là trung điểm của AC
=>\(MA=MC=\dfrac{AC}{2}=\dfrac{4}{2}=2\left(cm\right)\)
ΔABM vuông tại A
=>\(AB^2+AM^2=BM^2\)
=>\(BM=\sqrt{3^2+2^2}=\sqrt{13}\left(cm\right)\)
Xét ΔBAC có BM là đường trung tuyến
nên \(\overrightarrow{BC}+\overrightarrow{BA}=2\cdot\overrightarrow{BM}\)
=>\(\left|\overrightarrow{BC}+\overrightarrow{BA}\right|=2\cdot BM=2\sqrt{13}\left(cm\right)\)
b: Xét ΔABC có AI là đường trung tuyến
nên \(\overrightarrow{AB}+\overrightarrow{AC}=2\cdot\overrightarrow{AI}\)
=>\(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=2\cdot AI=2\cdot2,5=5\left(cm\right)\)
c: Gọi N là trung điểm của AB
=>\(AN=\dfrac{AB}{2}=1,5\left(cm\right)\)
ΔCAN vuông tại A
=>\(CA^2+AN^2=CN^2\)
=>\(CN=\sqrt{4^2+1,5^2}=\sqrt{18,25}=\dfrac{\sqrt{73}}{2}\)
Xét ΔCAB có CN là đường trung tuyến
nên \(\overrightarrow{CA}+\overrightarrow{CB}=2\cdot\overrightarrow{CN}\)
=>\(\left|\overrightarrow{CA}+\overrightarrow{CB}\right|=2\cdot CN=\sqrt{73}\left(cm\right)\)
d: \(2\overrightarrow{IA}-\overrightarrow{CA}=-2\overrightarrow{AI}+\overrightarrow{AC}\)
\(=-\overrightarrow{AB}-\overrightarrow{AC}+\overrightarrow{AC}=-\overrightarrow{AB}\)
=>\(\left|2\overrightarrow{IA}-\overrightarrow{CA}\right|=\left|-\overrightarrow{AB}\right|=AB=3\left(cm\right)\)
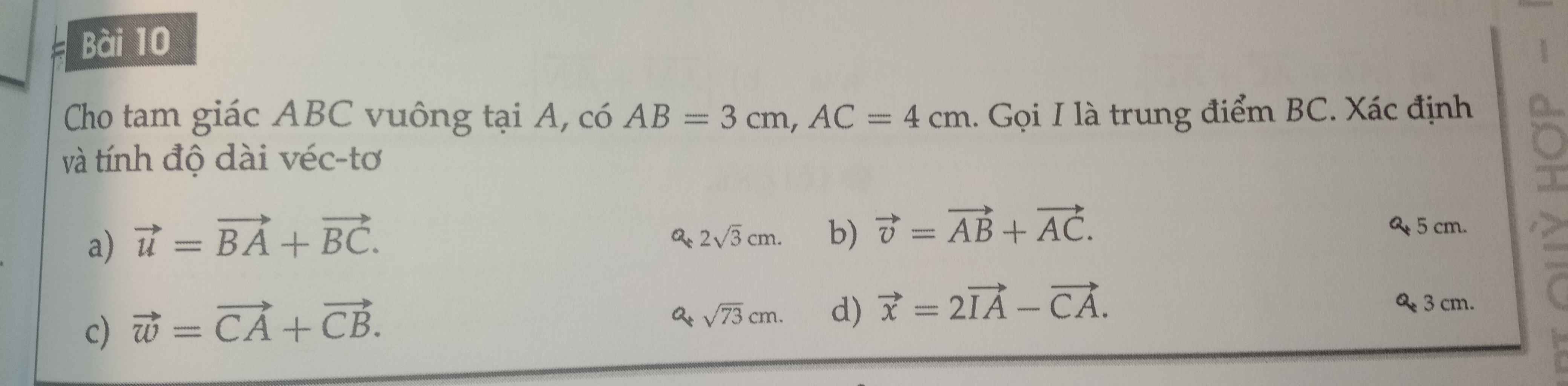đề bài đây ạ, hoc24 bị lỗi hay sao mà e không đính kèm được ảnh vào câu hỏi ạ
