a.
\(\sqrt{x-1}=1\)
\(x-1=1^2\)
\(x-1=1\)
\(x=2\) (thỏa mãn)
b.
\(\sqrt{x+2}=2\)
\(x+2=2^2\)
\(x+2=4\)
\(x=4-2=2\) (thỏa mãn)
c.
\(\sqrt{19-x}=19\)
\(19-x=19^2\)
\(19-x=361\)
\(x=19-361\)
\(x=-342\) (thỏa mãn)
d.
\(\sqrt{x^2+1}=3\)
\(x^2+1=3^2\)
\(x^2+1=9\)
\(x^2=8\)
\(x=\pm\sqrt{8}=\pm2\sqrt{2}\)
e.
\(x^2-2=0\)
\(x^2=2\)
\(x=\pm\sqrt{2}\)
g.
\(5-x^2=1\)
\(x^2=5-1\)
\(x^2=4\)
\(x=\pm\sqrt{4}\)
\(x=\pm2\)
h.
\(\left(1-x\right)^2=3\)
\(1-x=\pm\sqrt{3}\)
\(1-x=\sqrt{3}\) hoặc \(1-x=-\sqrt{3}\)
\(x=1-\sqrt{3}\) hoặc \(x=1-\left(-\sqrt{3}\right)\)
\(x=1-\sqrt{3}\) hoặc \(x=1+\sqrt{3}\)
f.
\(\left(x-1\right)^2+\dfrac{1}{7}=0\)
\(\left(x-1\right)^2=-\dfrac{1}{7}\)
Do \(-\dfrac{1}{7}< 0\) còn \(\left(x-1\right)^2\ge0;\forall x\)
nên pt đã cho vô nghiệm

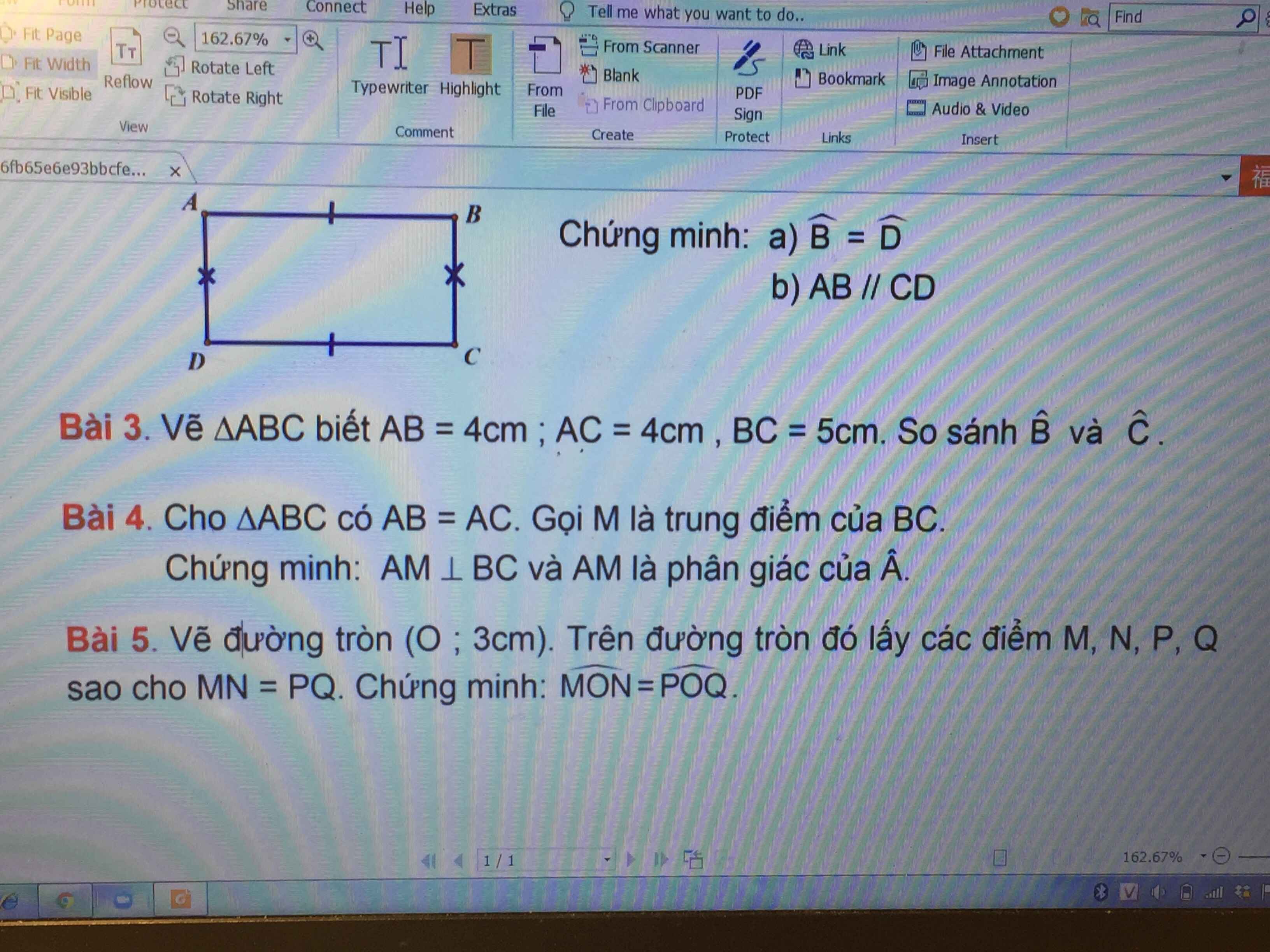
 Giải giúp bài 5
Giải giúp bài 5













 G
G
 Các bạn giải giúp mình bài 4 và bài 5 phần Tự luận nhé
Các bạn giải giúp mình bài 4 và bài 5 phần Tự luận nhé


