P1. \(\dfrac{2x+3}{5}-\dfrac{3x-5}{7}=\dfrac{2x+1}{3}\)
\(\Leftrightarrow
\dfrac{21\left(2x+3\right)}{105}-\dfrac{15\left(3x-5\right)}{105}=\dfrac{35\left(2x+1\right)}{105}\)
\(\Rightarrow
42x+63-45x+75=70x+35\)
\(\Leftrightarrow
-3x+138=70x+35\)
\(\Leftrightarrow
-3x-70x=-138+35\)
\(\Leftrightarrow
-73x=-103\)
\(\Leftrightarrow x=\dfrac{103}{73}\)
Vậy tập No của PT là \(S=\left\{\dfrac{103}{73}\right\}\)
phần còn lại mik chx lm ra :(
a) Ta có: \(\dfrac{2x+3}{5}-\dfrac{3x-5}{7}=\dfrac{2x+1}{3}\)
\(\Leftrightarrow\dfrac{21\left(2x+3\right)}{105}-\dfrac{15\left(3x-5\right)}{105}=\dfrac{35\left(2x+1\right)}{105}\)
\(\Leftrightarrow42x+63-45x+75=70x+35\)
\(\Leftrightarrow-3x+138-70x-35=0\)
\(\Leftrightarrow-73x+103=0\)
\(\Leftrightarrow-73x=-103\)
hay \(x=\dfrac{103}{73}\)
Vậy: \(S=\left\{\dfrac{103}{73}\right\}\)
b) ĐKXĐ: \(x\notin\left\{2;0\right\}\)
Ta có: \(\dfrac{x+2}{x-2}-\dfrac{2}{x^2-2x}=\dfrac{1}{x}\)
\(\Leftrightarrow\dfrac{x\left(x+2\right)}{x\left(x-2\right)}-\dfrac{2}{x\left(x-2\right)}=\dfrac{x-2}{x\left(x-2\right)}\)
Suy ra: \(x^2+2x-2-x+2=0\)
\(\Leftrightarrow x^2+x=0\)
\(\Leftrightarrow x\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\left(loại\right)\\x=-1\left(nhận\right)\end{matrix}\right.\)
Vậy:S={-1}
A.2x+3/3 - 3x-5/7 = 2x+1/3
<=>21(2x+3) - 15(3x-5) = 35(2x+1)
<=>42x+63 - 45x+75 = 70x+35
<=>-3x +138 = 70x+35
<=>-3x-70x = 35-138
<=>-73x = -103
<=>x = 103/73
Vậy S={103/73}
B. x+2/x-2 - 2/x^2-2x = 1/x (1)
ĐKXĐ: x khác 0, x khác 2
Từ (1)<=> x+2/x-2 - 2/x(x-2) = 1/x
=>x(x+2) - 2 = x-2
<=> x^2 + 2x - 2 - x +2 =0
<=> x^2 +x =0
<=> x(x+1)=0
chia ra 2 trường hợp nha bn
Trường hợp 1:<=>x=0
Trường hợp 2:<=> x+1=0
<=>x=0(loại)
<=>x=-1(t/m)
Vậy S={-1}
chỗ nào ko hỉu thì ns nha

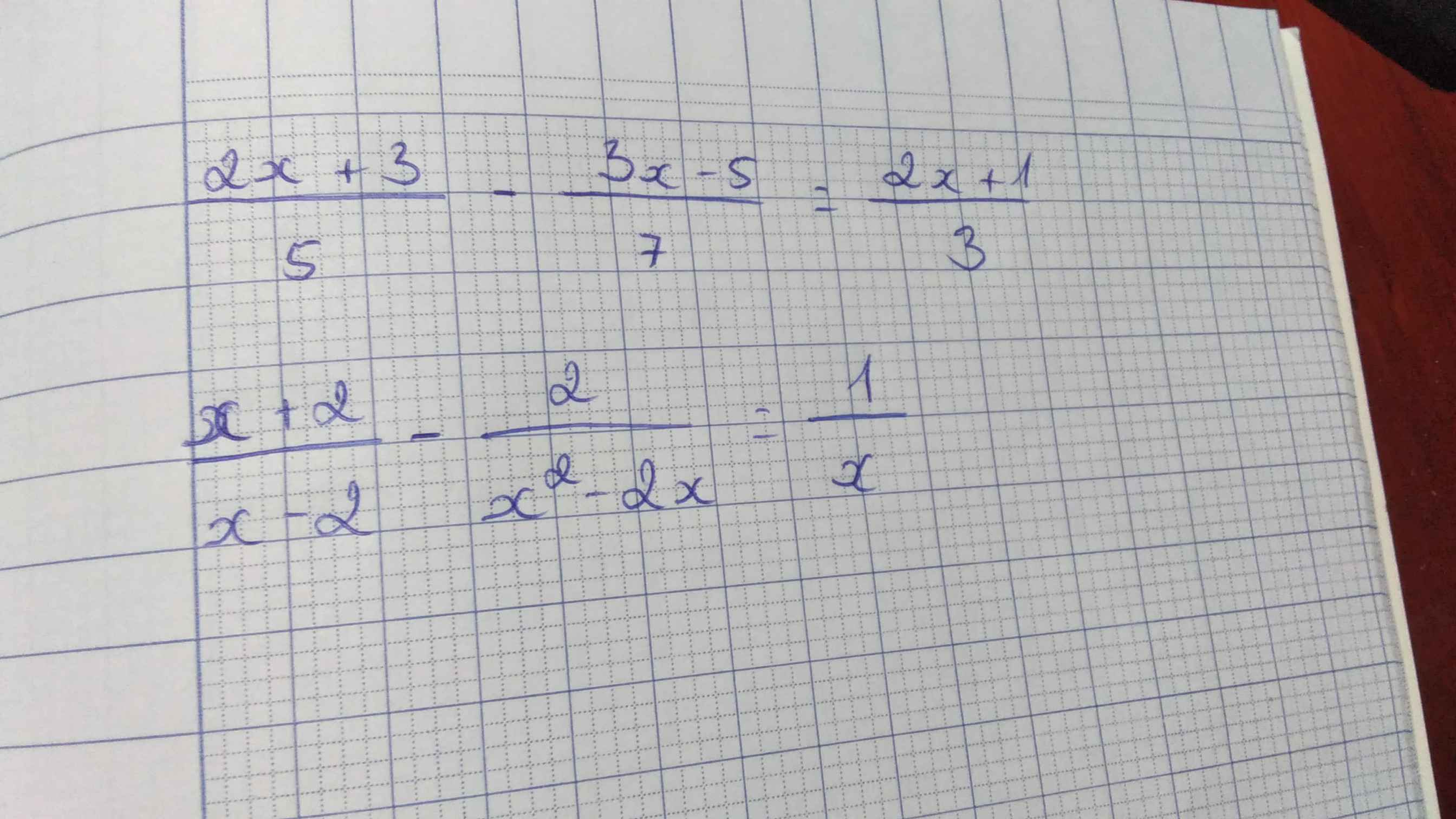








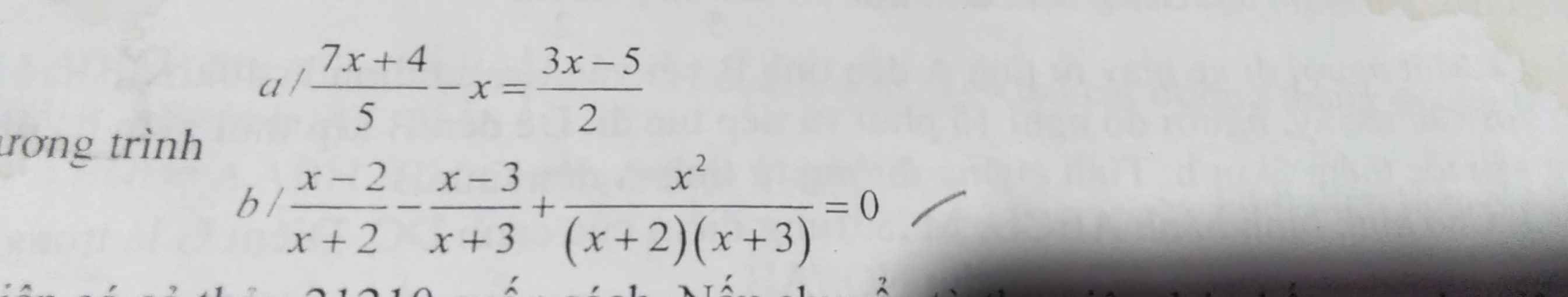





 ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn
ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn




