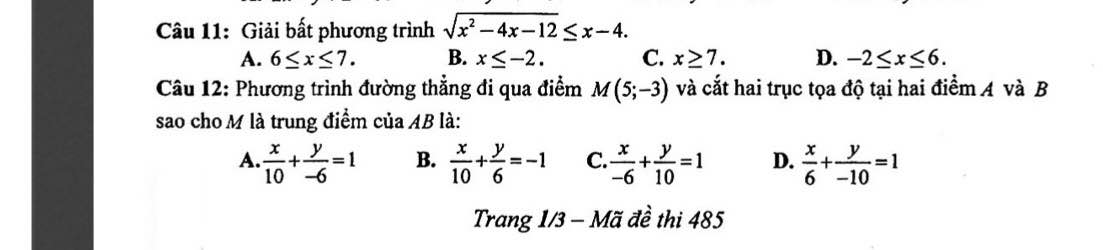2 câu a,b em giải đúng rồi
c. Sai
\(A\subset B\Leftrightarrow\left[{}\begin{matrix}1-m>3\\\dfrac{m+3}{2}< -3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m< -2\\m< -9\end{matrix}\right.\)
Kết hợp điều kiện \(A\ne\varnothing\Rightarrow\left[{}\begin{matrix}-\dfrac{1}{3}\le m< -2\\-\dfrac{1}{3}\le m< -9\end{matrix}\right.\)
\(\Rightarrow\) Ko tồn tại m thỏa mãn
Vậy ko có giá trị nguyên nào của m để \(A\subset B\)
d. Sai
\(A\cup B=R\Leftrightarrow\left\{{}\begin{matrix}1-m\le-3\\\dfrac{m+3}{2}\ge3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m\ge4\\m\ge3\end{matrix}\right.\)
\(\Rightarrow m\ge3\)
Vậy có vô số giá trị nguyên của m thỏa mãn

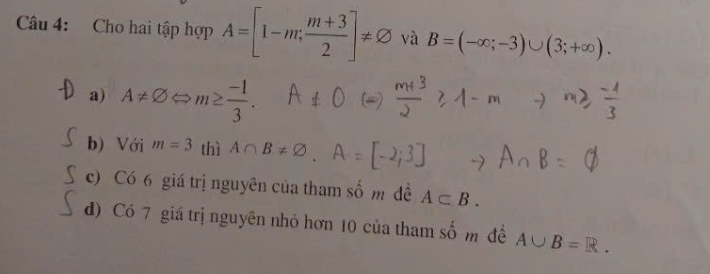








 Giải giúp mình phần trắc nghiệm với ạ
Giải giúp mình phần trắc nghiệm với ạ


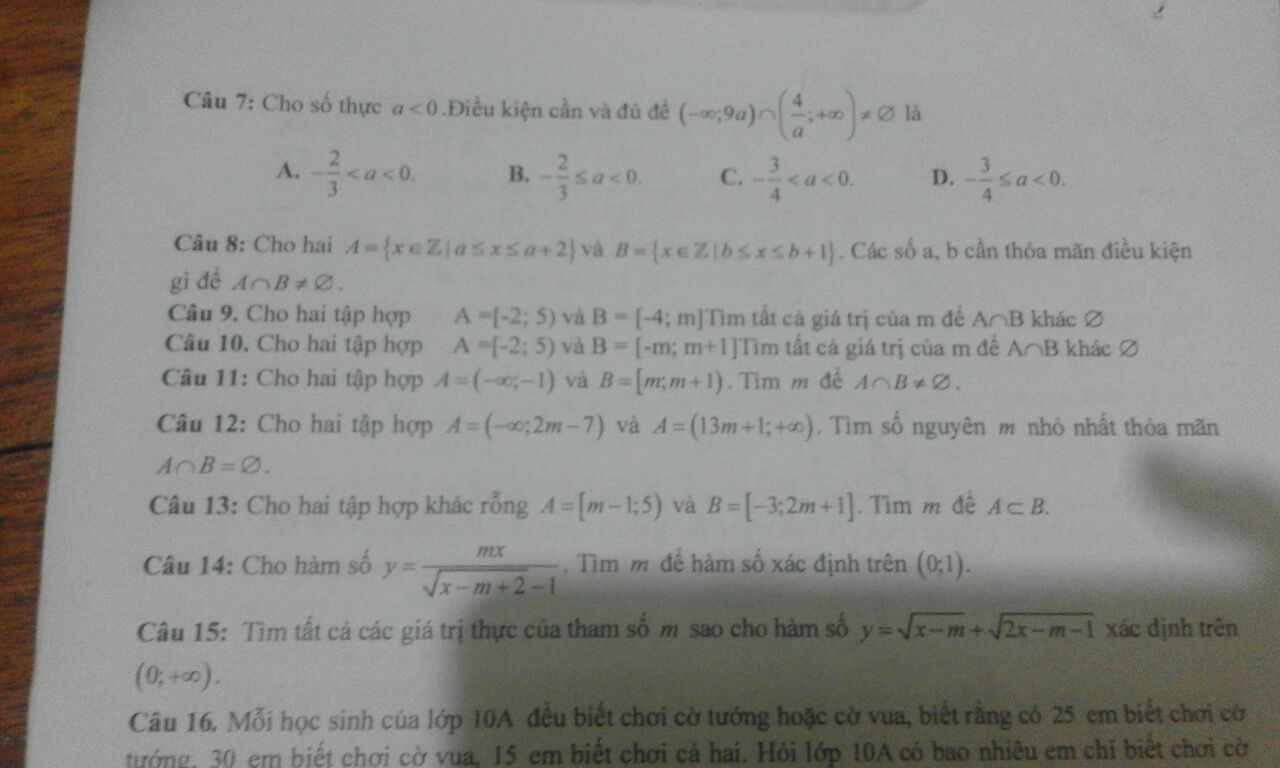 GIÚP MK VS!!! MAI MK PHẢI NỘP RỒI!!!!!!!!
GIÚP MK VS!!! MAI MK PHẢI NỘP RỒI!!!!!!!!