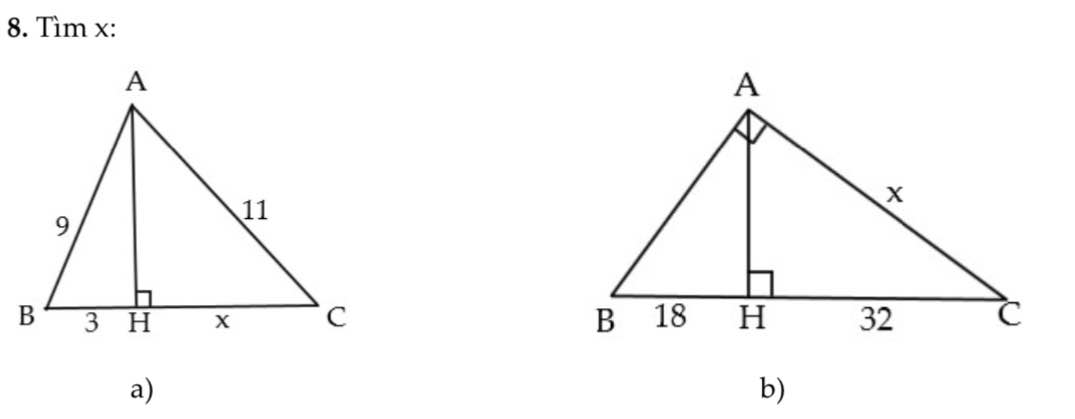
a) \(x^y+3=z\left(1\right)\)
- Với \(y=1\)
\(\left(1\right)\Rightarrow x+3=z\)
mà \(z\) là số nguyên tố
\(\Rightarrow x\) là số chẵn
\(\Rightarrow x=2\) (vì \(2\) là số nguyên tố)
\(\Rightarrow z=5\)
\(\Rightarrow\left(x;y;z\right)=\left(2;1;5\right)\)
- Với \(y>1\)
\(x^y\) là số lẻ (vì \(x\) là số nguyên tố lớn hơn \(2\))
\(\Rightarrow x^y+3=z\) là số chẵn lớn hơn \(3\) (Vô lý vì \(z\) là số nguyên tố)
\(\Rightarrow\) không tồn tại \(\left(x;y;z\right)\) trong trường hợp này
Vậy \(\left(1\right)\) có 1 nghiệm duy nhất là \(\left(x;y;z\right)=\left(2;1;5\right)\)
b) \(x^y+13=z\left(1\right)\)
- Với \(y=1\)
\(\left(1\right)\Rightarrow x+13=z\)
\(\Rightarrow x=2;y=15\left(ktm\right)\)
Vậy không có nghiệm trong trường hợp này
- Với \(y>1\)
\(x^y\) là số lẻ
\(\Rightarrow x^y+13=z\) là số chẵn lớn hơn \(13\) ((vô lý vì \(z\) là số nguyên tố)
Vậy không tồn tại nghiệm trong trường hợp này
Tốm lại \(\left(1\right)\) không có nghiệm là số nguyên tố
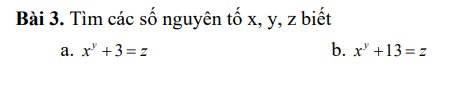
Giúp mình với aa (Giải chi tiết + nếu được thì thêm lời giải thích ở cuối bài làm giúp mình nha 
)
