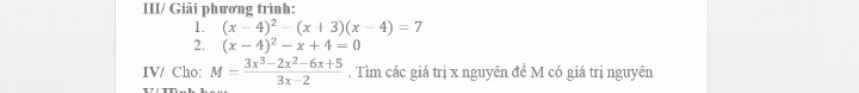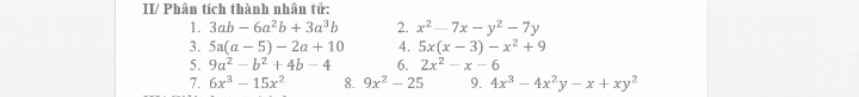a/
\(\widehat{BAE}+\widehat{DAE}=\widehat{BAD}=90^o\)
\(\widehat{DAF}+\widehat{DAE}=\widehat{FAE}=90^o\)
\(\Rightarrow\widehat{BAE}=\widehat{DAF}\) (cùng phụ với \(\widehat{DAE}\) ) (1)
\(AB=AD\) (cạnh hình vuông) (2)
Xét tg vuông ABE và tg vuông ADF
Từ (1) và (2) => tg ABE = tg ADF (Hai tg vuông có cạnh góc vuông và góc nhọn tương ứng bằng nhau)
\(\Rightarrow AE=AF\) (đpcm)
b/
AE=AF (cmt) => tg AEF là tg cân tại A
I là trung điểm EF (gt)
=> AI là trung tuyến thuộc EF => \(AI\perp EF\) (tring tg cân đường trung tuyến xp từ đỉnh tg cân đồng thời là đường cao)
\(\Rightarrow GK\perp EF\) (3)
Xét tg EIG và tg FIK có
\(\widehat{EIG}=\widehat{FIK}\) (góc đối đỉnh) (4)
EG//AB; AB//CD => EG//CD => EG//FK (5)
\(\Rightarrow\widehat{GEI}=\widehat{KFI}\) (góc so le trong) (6)
\(IE=IF\) (gt) (7)
Từ (4) (6) (7) => tg EIG = tg FIK (g.c.g) => EG = FK (8)
Từ (5) và (8) => EGFK là hình bình hành (Tứ giác có cặp cạnh đối // và = nhau là hình bình hành) (9)
Từ (3) và (9) => EGFK là hình thoi (hình bình hành có hai đường chéo vuông góc với nhau là hình thoi) (đpcm)
c/
Ta có tg AEF cân tại A (cmt); AI là trung tuyến thuộc EF (cmt)
=> AI là phân giác \(\widehat{EAF}\) (trong tg cân đường trung tuyến xp từ đỉnh tg cân đồng thời là đường phân giác của góc ở đỉnh)
Mà \(\widehat{EAF}=90^o\)
\(\Rightarrow\widehat{FAK}=45^o\)
\(\widehat{ACF}=45^o\)
\(\Rightarrow\widehat{FAK}=\widehat{ACF}=45^o\)
Xét tg AKF và tg ACF có
\(\widehat{FAK}=\widehat{ACF}=45^o\)
\(\widehat{AFC}\) chung
=> tg AKF đồng dạng với tg CAF (g.g.g)
d/