a: ĐKXĐ: a<>-1
Để \(\dfrac{a^2+a+3}{a+1}\in Z\) thì \(a^2+a+3⋮a+1\)
=>\(a\left(a+1\right)+3⋮a+1\)
=>\(3⋮a+1\)
=>\(a+1\in\left\{1;-1;3;-3\right\}\)
=>\(a\in\left\{0;-2;2;-4\right\}\)
b: x-2xy+y=0
=>\(x\left(1-2y\right)+y-0,5=-0,5\)
=>\(-2x\left(y-0,5\right)+\left(y-0,5\right)=-0,5\)
=>\(\left(y-0,5\right)\left(-2x+1\right)=-0,5\)
=>\(\left(2y-1\right)\left(-2x+1\right)=-1\)
=>(2y-1)(2x-1)=1
=>\(\left(2x-1;2y-1\right)\in\left\{\left(1;1\right);\left(-1;-1\right)\right\}\)
=>\(\left(x;y\right)\in\left\{\left(1;1\right);\left(0;0\right)\right\}\)

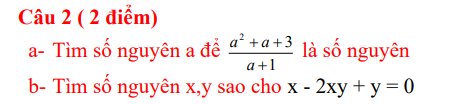




 Giúp mình với aa (Giải chi tiết + nếu được thì thêm lời giải thích ở cuối bài làm giúp mình nha
Giúp mình với aa (Giải chi tiết + nếu được thì thêm lời giải thích ở cuối bài làm giúp mình nha 






 Giải chi tiết hộ mình nha!!!
Giải chi tiết hộ mình nha!!!


