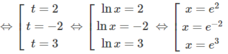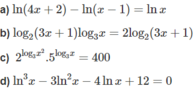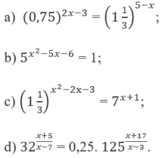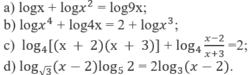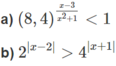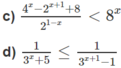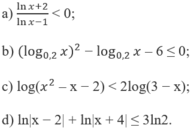Question

Giải các phương trình sau:

Answer 1

a) Với điều kiện x > 1 ta có phương trình:

ln(4x + 2) = ln[x(x − 1)]

⇔ 4x + 2 = x 2  – x ⇔  x 2  – 5x – 2 = 0

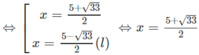
b) Với điều kiện x > 0, ta có phương trình

log 2 ( 3 x + 1 ) [ log 3 x - 2 ] = 0

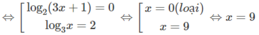
c) Với điều kiện x > 0, ta có phương trình:

4 log 3 x . 5 log 3 x  = 400

⇔ 20 log 3 x  = 20 2

⇔ log 3 x = 2 ⇔ x = 9 (thỏa mãn điều kiện)

d) Đặt t = lnx(x > 0), ta có phương trình:

t 3  – 3 t 2  – 4t + 12 = 0 ⇔ (t – 2)(t + 2)(t – 3) = 0