Cách 1
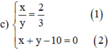
Từ (1) ta rút ra được 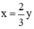 (*)
(*)
Thế (*) vào phương trình (2) ta được :
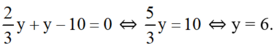
Thay y = 6 vào (*) ta được x = 4.
Vậy hệ phương trình có nghiệm duy nhất (x ; y) = (4 ; 6).
Cách 2
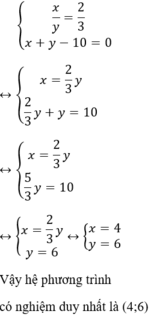
Cách 1
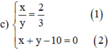
Từ (1) ta rút ra được 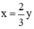 (*)
(*)
Thế (*) vào phương trình (2) ta được :
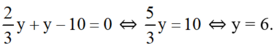
Thay y = 6 vào (*) ta được x = 4.
Vậy hệ phương trình có nghiệm duy nhất (x ; y) = (4 ; 6).
Cách 2
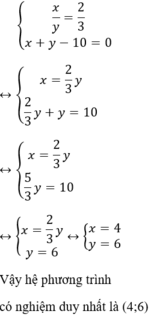
Giải các hệ phương trình sau bằng phương pháp thế: x - 2 2 y = 5 x 2 + y = 1 - 10
Giải các hệ phương trình sau bằng phương pháp thế: x - y = 3 3 x - 4 y = 2
Giải các hệ phương trình sau bằng phương pháp thế:
a ) x + y 5 = 0 x 5 + 3 y = 1 − 5 b ) ( 2 − 3 ) x − 3 y = 2 + 5 3 4 x + y = 4 − 2 3
Giải các hệ phương trình sau bằng phương pháp thế:
a ) 3 x − y = 5 5 x + 2 y = 23 b ) 3 x + 5 y = 1 2 x − y = − 8 c ) x y = 2 3 x + y − 10 = 0
Giải các hệ phương trình sau bằng phương pháp thế:
a ) x 2 − y 3 = 1 x + y 3 = 2 b ) x − 2 2 y = 5 x 2 + y = 1 − 10 c ) ( 2 − 1 ) x − y = 2 x + ( 2 + 1 ) y = 1
Giải các hệ phương trình sau bằng phương pháp thế:
a ) x − y = 3 3 x − 4 y = 2 b ) 7 x − 3 y = 5 4 x + y = 2 c ) x + 3 y = − 2 5 x − 4 y = 11
Giải hệ phương trình sau bằng phương pháp thế (biểu diễn y theo x từ phương trình thứ hai của hệ)
4 x − 5 y = 3 3 x − y = 16
Giải hệ phương trình sau bằng phương pháp thế (biểu diễn y theo x từ phương trình thứ hai của hệ) 4 x - 5 y = 3 3 x - y = 16
giải hệ phương trình bằng phương pháp thế
\(\left\{{}\begin{matrix}\dfrac{x}{2}+\dfrac{y}{2}=1\\x+y=3\end{matrix}\right.\)