Đặt t = logx với điều kiện t ≠ 5, t ≠ −1 ta có:
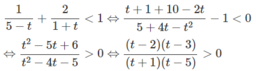
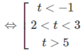
Suy ra log x < -1 hoặc 2 < log x < 3 hoặc log x > 5.
Vậy x < 1/10 hoặc 100 < x < 1000 hoặc x > 100 000.
Đặt t = logx với điều kiện t ≠ 5, t ≠ −1 ta có:
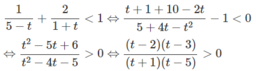
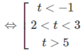
Suy ra log x < -1 hoặc 2 < log x < 3 hoặc log x > 5.
Vậy x < 1/10 hoặc 100 < x < 1000 hoặc x > 100 000.
Giải các bất phương trình sau: (x − 5)(logx + 1) < 0
Giải các phương trình logarit sau: log x + log x 2 = log 9 x
Giải phương trình logx = log(x + 3) - log(x - 1)
A. x = 1
B. x = 3
C. x = 4
D. x = -1, x = 3
Giải bất phương trình log x + log ( x + 9 ) > 11
A. x > 1
B. x < 0 hoặc x > 3
C. x < 1 hoặc x > 2
D. 0 < x < 1 hoặc 2 < x < 3
Giải các bất phương trình logarit sau: log 3 x - 3 + log 3 x - 5 < 1
Giải các bất phương trình logarit sau: log 1 3 x - 1 ≥ - 2
Giải các bất phương trình sau:
a) (2x − 7)ln(x + 1) > 0;
b) (x − 5)(logx + 1) < 0;
c) 2 log 3 2 x + 5 log 2 2 x + log 2 x – 2 ≥ 0
d) ln(3 e x − 2) ≤ 2x
Giải các bất phương trình logarit sau: 4 log 4 x - 33 log x 4 ≤ 1
Tìm tập nghiệm của bất phương trình log ( x - 21 ) < 2 - log x
A. (-4; 25)
B. (0; 25)
C. (21; 25)
D. (25; +∞)