Điều kiện xác định x ≠ 0; x ≠ –3; x ≠ –4.
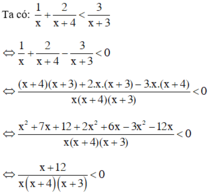
Đặt 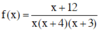 . Ta có bảng xét dấu sau:
. Ta có bảng xét dấu sau:

Dựa vào bảng xét dấu ta thấy
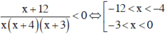
Vậy tập nghiệm của bất phương trình là S = (–12; –4) ∪ (–3; 0).
Điều kiện xác định x ≠ 0; x ≠ –3; x ≠ –4.
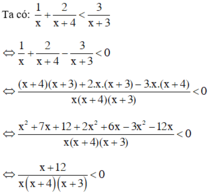
Đặt 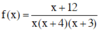 . Ta có bảng xét dấu sau:
. Ta có bảng xét dấu sau:

Dựa vào bảng xét dấu ta thấy
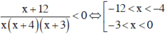
Vậy tập nghiệm của bất phương trình là S = (–12; –4) ∪ (–3; 0).
Giải bất phương trình: \(\sqrt[3]{x+1}+\sqrt{2x+4}< 3-x\sqrt{2}\)
1/ Với giá trị nào của x thì 2 bất phương trình sau đây tương đương: (a-1)x - a+3>0 và ( a+1)x-a+2>0
2/ Bất phương trình: 5x/5 - 13/21 + x/15 < 9/25- 2x/35 có nghiệm là....
3/ Bất phương trình: 5x-1 < 2x/5 + 3 có nghiệm là...
4/ Bất phương trình: (x+4/x^2-9) -(2/x+3) < (4x/3x-x^2) có nghiệm nguyên lớn nhất là...
5/ Các nghiệm tự nhiên bé hơn 4 của bất phương trình (2x/5) -23 < 2x -16
6/ Các nghiệm tự nhiên bé hơn 6 của bất phương trình: 5x - 1/3 > 12 - 2x/3
7/ Bất phương trình: 2(x-1) - x > 3(x-1) - 2x-5 có tập nghiệm là...
8/ Bất phương trình: (3x+5/2) -1< (x+2/3)+x có tập nghiệm là...
9/ Bất phương trình: /x+2/ - /x-1/ < x - 3/2 có tập nghiệm là
10/ Bất phương trình: /x+1/ + /x-4/ > 7 có nghiệm nguyên dương nhỏ nhất là....
Giải các phương trình, bất phương trình sau:
1) \(\sqrt{3x+7}-5< 0\)
2) \(\sqrt{-2x-1}-3>0\)
3) \(\dfrac{\sqrt{3x-2}}{6}-3=0\)
4) \(-5\sqrt{-x-2}-1< 0\)
5) \(-\dfrac{2}{3}\sqrt{-3-x}-3>0\)
\(\left(x-2\right)\sqrt{x^2-2x-3}\le x^2-4\)
Giải bất phương trình
1.Giải bất phương trình: 3* căn[1-(3/x)] + căn[3x-(27/x)] >= x
2. Tìm m để bất phương trình [(10-m)x^2-2(m+2)x+1]/[căn(x^2-2x+2] < 0 có nghiệm
Cảm ơn nhiều những ai giúp em ạ!
Giải các bất phương trình sau:
a)\(\left(x^2+3x-4\right)\left(3-2x\right)\)<0
b) \(\dfrac{x^2+3x+4}{x^2-2}\ge0\)
c) \(\dfrac{x\left(x^2+4x+4\right)}{x^2-1}\ge0\)
Giải các bất phương trình a (x-1)(2-x)>0 b x2 -4x+3
Giải bất phương trình sau: (2x - 1)(x + 3) - 3x + 1 ≤ (x - 1)(x + 3) + x2 - 5
Giải bất phương trình
(3)/(x-2) > hoặc =(5)/(2x-1)
Giải các bất phương trình sau:
a) \(\left(x^2+3x-4\right)\left(3-2x\right)< 0\)
\(\dfrac{x^2+3x+4}{x^2-2}\ge0\)
\(\dfrac{x\left(x^2+4x+4\right)}{x^2-1}\ge0\)
b) \(\dfrac{3x-2}{2-x}\le-x\)
c) \(\dfrac{x-3}{x+1}>\dfrac{x+4}{x+2}\)
d) \(\dfrac{x+2}{x-2}-\dfrac{x+3}{x-2}>1\)
e) \(|2x-3|>x+1\)
f) \(|2x-5|\le x+1\)
g) \(x-4-|x^2+3x-4|>0\)
h) \(\left|x^2+4x+3\right|>\left|x^2-4x-5\right|\)