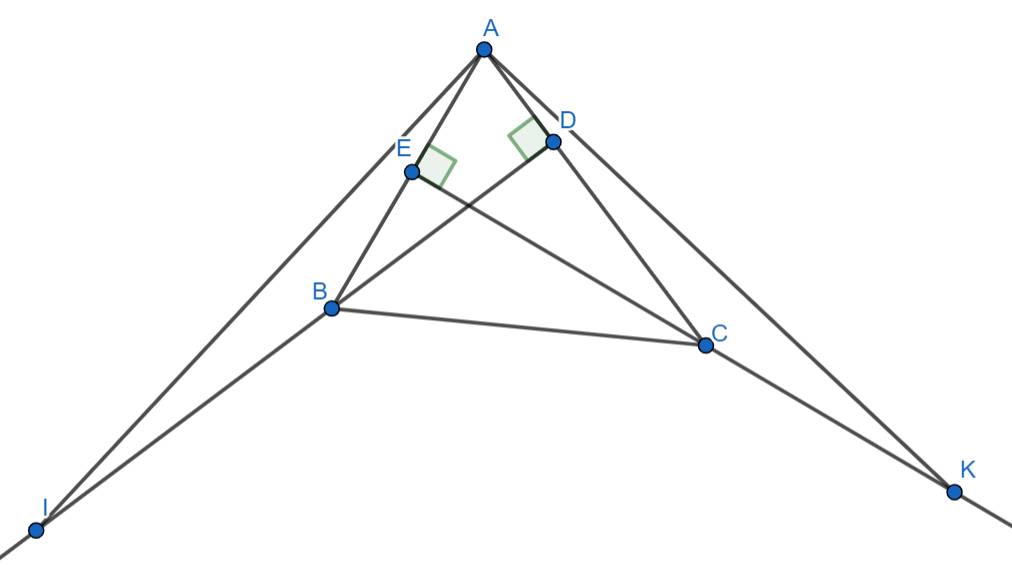
Xét \(\Delta ABD\) vuông tại D có: \(\widehat{ABD}+\widehat{BAC}=90^\circ\) (t/c)
Xét \(\Delta ACE\) vuông tại E có: \(\widehat{ACE}+\widehat{BAC}=90^\circ\) (t/c)
Suy ra: \(\widehat{ABD}=\widehat{ACE}\)
Mặt khác: \(\left\{{}\begin{matrix}\widehat{ABD}+\widehat{ABI}=180^{\circ}\left(\text{hai góc kề bù}\right)\\\widehat{ACE}+\widehat{KCA}=180^{\circ}\left(\text{hai góc kề bù}\right)\end{matrix}\right.\)\(\Rightarrow \widehat{ABI}=\widehat{KCA}\)
Xét \(\Delta AIB\) và \(\Delta KAC\) có: \(\left\{{}\begin{matrix}AB=KC\left(gt\right)\\\widehat{ABI}=\widehat{KCA}\left(cmt\right)\\IB=AC\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow \Delta AIB=\Delta KAC\text{ (c.g.c)}\Rightarrow AI=KA\)
\(\rightarrow\) Chọn D. AI = AK