Chọn: D
Hàm số y = x - 1 x + 1 xác định trên 0 ; 3
Ta có y ' = 2 x + 1 2 > 0 ∀ x ∈ 0 ; 3
Do đó hàm số đồng biến trên 0 ; 3
![]()
Chọn: D
Hàm số y = x - 1 x + 1 xác định trên 0 ; 3
Ta có y ' = 2 x + 1 2 > 0 ∀ x ∈ 0 ; 3
Do đó hàm số đồng biến trên 0 ; 3
![]()
Xét tính đồng biến, nghịch biến và tính giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
a) y = x2 trên đoạn [-3; 0];
b) y = trên đoạn [3; 5].
Cho hàm số f(x) liên tục trên (0;+ ∞ ) thỏa mãn 3x.f(x) - x 2 f ' ( x ) = 2 f 2 ( x ) , với f(x) ≠ 0, ∀ x ∈ (0;+ ∞ ) và f(1) = 1 3 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = f(x) trên đoạn [1;2]. Tính M + m.
A. 9 10
B. 21 10
C. 7 3
D. 5 3
Giá trị nhỏ nhất của hàm số y = x - 1 x + 1 trên đoạn [0; 3] là:
A. m i n 0 ; 3 = - 3
B. m i n 0 ; 3 = 1 2
C. m i n 0 ; 3 = - 1
D. m i n 0 ; 3 = 1
Giá trị nhỏ nhất của hàm số y = x - 1 x + 1 trên đoạn [0; 3] là:
A. m i n 0 ; 3 y = - 3
B. m i n 0 ; 3 y = 1 2
C. m i n 0 ; 3 y = - 1
D. m i n 0 ; 3 y = 1
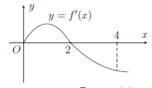
Cho hàm số f(x) có đồ thị của hàm số f'(x) như hình vẽ. Biết f(0) + f(1) - 2f(2) = f(4) - f(3). Giá trị nhỏ nhất m, giá trị lớn nhất M của hàm số f(x) trên đoạn [0;4] là
A. m = f(4), M = f(1)
B. m = f(4), M = f(2)
C. m = f(1), M = f(2)
D. m = f(0), M = f(2)
Cho hàm số y = x 4 - 4 x 3 + 4 x 2 + a . Gọi M; m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên đoạn [0; 2] . Có bao nhiêu số nguyên a thuộc đoạn [ -3; 3] sao cho M≤ 2m?
A. 4
B. 5
C. 6
D. 3
Cho hàm số f(x) = 2 x + m x + 1 với m là tham số thực. Tìm tất cả các giá trị của m > 1 để hàm số có giá trị lớn nhất trên đoạn [ 0; 4] nhỏ hơn 3.
A. 1<m< 3
B. m ∈ ( 1 ; 3 5 - 4 )
C. m ∈ ( 1 ; 5 )
D. 1<m≤ 4
Cho hàm số f(x) có đạo hàm là hàm f'(x). Đồ thị hàm số f'(x) như hình vẽ bên. Biết rằng f(0) + f(1) - 2f(2) = f(4) - f(3). Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của f(x) trên đoạn [0;4].

A. m = f(4), M = f(2)
B. m = f(1), M = f(2)
C. m = f(4), M = f(1)
D. m = f(0), M = f(2)
Giá trị nhỏ nhất của hàm số y = - x + 1 2 x + 3 trên đoạn [0; 2] là
A. ![]() .
.
B. ![]() .
.
C. 2.
D. 0.
Cho hàm số y= x3- 3x+ 1 . Tìm tìm tập hợp tất cả giá trị m> 0 , để giá trị nhỏ nhất của hàm số trên D= [m+ 1; m+ 2] luôn bé hơn 3 là:
A. (0; 1)
B. ( 1 2 ; 1)
C. (2; 3)
D. (0; 2)