Chọn C
Lưu ý: Hàm số liên trục trên một Đoạn thì luôn có GTLN và GTNN trên đoạn đó Nên áp dụng bài toán tìm GTLN, GTNN của hàm số trên một đoạn, không lập BBT của hàm sô.
Hàm số y = - x 2 + x - 6 x + 1 liên tục trên đoạn [0;3]
![]()
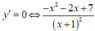

![]()
![]()
![]()
Chọn C
Lưu ý: Hàm số liên trục trên một Đoạn thì luôn có GTLN và GTNN trên đoạn đó Nên áp dụng bài toán tìm GTLN, GTNN của hàm số trên một đoạn, không lập BBT của hàm sô.
Hàm số y = - x 2 + x - 6 x + 1 liên tục trên đoạn [0;3]
![]()
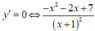

![]()
![]()
![]()
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
a) f(x) = ( 25 - x 2 ) trên đoạn [-4; 4]
b) f(x) = | x 2 – 3x + 2| trên đoạn [-10; 10]
c) f(x) = 1/sinx trên đoạn [π/3; 5π/6]
d) f(x) = 2sinx + sin2x trên đoạn [0; 3π/2]
Giá trị lớn nhất của hàm số y = - x 2 + 4x - 5 trên đoạn [0;3] bằng:
A. -1 B. 1
C. 2 D. 0
Giá trị lớn nhất của hàm số y = - x 2 + 4x - 5 trên đoạn [0;3] bằng:
A. -1 B. 1
C. 2 D. 0
Cho hàm số y=f(x) nhận giá trị dương và có đạo hàm liên tục trên đoạn [0;3] thoả mãn f(0)=3, f(3)=8 và ∫ 0 3 ( f ' ( x ) ) 2 f ( x ) + 1 d x = 4 3 Giá trị của f(2) bằng
A. 64 9
B. 55 9
C. 16 3
D. 19 3
Tính giá trị lớn nhất và nhỏ nhất của hàm số:
y = 2 - x 1 - x trên các đoạn [2 ; 4] và [-3 ; -2]
Giá trị nhỏ nhất của hàm số y = x - 1 x + 1 trên đoạn 0 ; 3 là:
A. m i n [ 0 ; 3 ] y = 1 2
B. m i n [ 0 ; 3 ] y = 1
C. m i n [ 0 ; 3 ] y = - 3
D. m i n [ 0 ; 3 ] y = - 1
Cho hàm số y = x - m 2 x + 8 với m là tham số thực. Giả sử m 0 là giá trị dương của tham số m để hàm số có giá trị nhỏ nhất trên đoạn [0;3] bằng -3. Giá trị m 0 thuộc khoảng nào trong các khoảng cho dưới đây?
A. (20;25)
B. (5;6)
C. (6;9)
D. (2;5)
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x)= x^3-3x^2+2 trên đoạn [-1,2] . Tính giá trị biểu thức P= M-2m A. 3√2-3 B. 2√2-5 C. 3√3-5 D. 3√3-3
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số sau trên đoạn [0;2] bằng
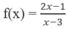
A. 1/3 và -3 B. 3/2 và -1
C. 2 và -3 D. 1/2 và 5