f ( 2 ) = 5; f ( - 2 )= 1; f ( 0 ) = 5; f ( 2 ) = 1; f ( 3 ) = 50
Đáp án cần chọn là A
f ( 2 ) = 5; f ( - 2 )= 1; f ( 0 ) = 5; f ( 2 ) = 1; f ( 3 ) = 50
Đáp án cần chọn là A
Giá trị lớn nhất của hàm số f ( x ) = x 4 - 4 x 2 + 5 trên đoạn [-2;3] bằng
A. 50.
B. 5.
C. 1.
D. 22
Giá trị lớn nhất của hàm số f ( x ) = x 4 - 4 x 2 + 5 trên đoạn [-2;3] bằng:
A. 50
B. 5
C. 1
D. 122
Cho hàm số y=f(x) có bảng biến thiên như sau:
Tích của giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=f(x) trên đoạn [-2;3] bằng
A. -6
B. -8
C. -12
D. -9
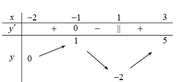
Cho hàm số f x = a x + b c x + d với a , b , c , d ∈ R có đồ thị hàm số y=f'(x) như hình vẽ bên. Biết rằng giá trị lớn nhất của hàm số y=f(x) trên đoạn [-3;-2] bằng 8. Giá trị của f(2) bằng.

A. 2
B. 5
C. 4
D. 6
Cho hàm số y=f(x), xÎ[-2;3] có đồ thị như hình vẽ. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) trên đoạn Î[-2;3]. Giá trị của S=M+m là
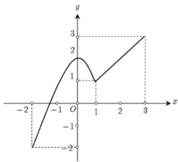
A. 6
B. 1
C. 5
D. 3
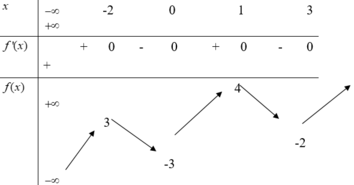
Cho hàm số f (x) xác định và liên tục trên đoạn [-2;3] và có bảng biến thiên như hình vẽ sau
Giá trị nhỏ nhất của hàm số f (x) trên đoạn [-2;3] bằng
A. -2
B. 5.
C. 0.
D. 1
Tích của giá trị nhỏ nhất và giá trị lớn nhất của hàm số f(x)=x+4/x trên đoạn [1;3] bằng.
A. 20.
B. 6.
C. 65/3.
D. 52/3.
Cho hàm số y = − x 2 + 2 , khi x ≤ 1 x , k h i x > 1 . Tìm giá trị lớn nhất của hàm số trên đoạn − 2 ; 3
A. max − 2 ; 3 y = − 2
B. max − 2 ; 3 y = 2
C. max − 2 ; 3 y = 1
D. max − 2 ; 3 y = 3
Cho hàm số có đồ thị y = f ( x ) như dưới đây. Hãy chỉ ra giá trị lớn nhất và nhỏ nhất của hàm số trên đoạn - 2 ; 3
A. m i n - 2 ; 3 f ( x ) = 1 và m i n - 2 ; 3 f ( x ) = 2
B. m i n - 2 ; 3 f ( x ) = - 2 và m i n - 2 ; 3 f ( x ) = 3
C. m i n - 2 ; 3 f ( x ) = 1 và m i n - 2 ; 3 f ( x ) = 3
D. m i n - 2 ; 3 f ( x ) = - 2 và m i n - 2 ; 3 f ( x ) = - 2
Cho các mệnh đề :
1) Hàm số y=f(x) có đạo hàm tại điểm x 0 thì nó liến tục tại x 0 .
2) Hàm số y=f(x) liên tục tại x 0 thì nó có đạo hàm tại điểm x 0 .
3) Hàm số y=f(x) liên tục trên đoạn [a;b] và f(a).f(b)<0 thì phương trình f(x) có ít nhất một nghiệm trên khoảng (a;b).
4) Hàm số y=f(x) xác định trên đoạn [a;b] thì luôn tồn tại giá trị lớn nhất và giá trị nhỏ nhất trên đoạn đó.
Số mệnh đề đúng là:
A. 2
B. 4
C. 3
D. 1