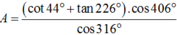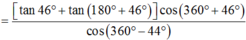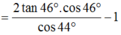Các câu hỏi tương tự
Tìm các giá trị lượng giác còn lại biết:
a) Cho sin \(x=-\dfrac{4}{5}\)và \(90^o< x< 180^o\)
b) Cho \(\sin x=\dfrac{\sqrt{3}}{2}\)và \(270^o< x< 360^o\)
c) Cho \(\cos x=-\dfrac{1}{3}\)và \(0^o< x< 90^o\)
Cho tam giác ABC nội tiếp (O;R) có H là trực tâm, G là trọng tâm.Chứng minh rằng:
a)\(P_{G/\left(O\right)}=-\frac{1}{9}\left(AB^2+AC^2+BC^2\right)\)
b)\(P_{H/\left(O\right)=-8R.\cos A.\cos B.\cos C}\)
Tìm góc a, \(0^o\le a\le180^o\) trong mỗi trường hợp sau:
a) sin a = 1/2
b) cos a = 0
c) tan a = \(-\sqrt{3}\)
Cho sin = 1/3 với 90\(^o\)<\(\alpha\)<180\(^o\). Tính cos \(\alpha\) và tan (180\(^o\) - \(\alpha\))
Cho tam giác ABC. Chứng minh rằng:a) Nếu (a+b+c).(b+c-a)3bc thì widehat{A}60^ob) Nếu frac{b^3+c^3-a^3}{b+c-a}a2 thì widehat{A}60^oc) Nếu cos.(A+C)+3.cosB1 thì widehat{B}60^od) Nếu b.(b2-a2)c.(a2-c2) thì widehat{A}60^o
Đọc tiếp
Cho tam giác ABC. Chứng minh rằng:
a) Nếu (a+b+c).(b+c-a)=3bc thì \(\widehat{A}=60^o\)
b) Nếu \(\frac{b^3+c^3-a^3}{b+c-a}\)=a2 thì \(\widehat{A}=60^o\)
c) Nếu cos.(A+C)+3.cosB=1 thì \(\widehat{B}=60^o\)
d) Nếu b.(b2-a2)=c.(a2-c2) thì \(\widehat{A}=60^o\)
Cho lục giác đều $A B C D E F$ tâm $O$. Chứng minh: $\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C}+\overrightarrow{O D}+\overrightarrow{O E}+\overrightarrow{O F}=\overrightarrow{0}$.
Bài 3. (1 điểm) Cho hình vuông $ABCD$ cạnh $a$ có tâm $O$ là giao điểm của hai đường chéo.
a) Tính độ dài của $\overrightarrow{OA}-\overrightarrow{CB}$ .
b) Chứng minh rằng $\overrightarrow{DA}-\overrightarrow{DB}+\overrightarrow{DC}=\overrightarrow{0}$.
Cho ∆ABC đều cạnh bằng a , chứng minh nội tiếp đường tròn (O) . Điểm M thuộc (O) sao cho T=| vectơ MA+ vectơ MB - vectơ MC | lớn nhất. Khi đó giá trị của T bằng bao nhiêu?
$\dfrac{\sin C}{\sin B}=2\cos A$
$\to \sin C=2\sin B\cos A$
$\to \sin C=\sin (A+B)-\sin (A-B)$
$\to \sin C=\sin(180^o-C)-\sin(A-B)$
$\to \sin C=\sin(C)-\sin(A-B)$
$\to \sin(A-B)=0$
$\to A-B=0$
$\to A=B$
$\to \Delta ABC$ cân tại $C$
Câu 36. Bác Hùng dùng $200$ m hàng rào dây thép gai để rào miếng đất đủ rộng thành một mảnh vườn hình chữ nhật.
a) Tìm công thức tính diện tích $S(x)$ của mảnh vườn hình chữ nhật rào được theo chiều rộng $x$ (m) của mảnh vườn đó.
b) Tìm kích thước của mảnh vườn hình chữ nhật có diện tích lớn nhất có thể rào được.