Hai góc bù nhau là hai góc có tổng bằng 180 o
Giả thiết của định lý: “Hai góc cùng bù với một góc thứ ba thì bằng nhau” là
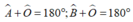
Chọn đáp án A
Hai góc bù nhau là hai góc có tổng bằng 180 o
Giả thiết của định lý: “Hai góc cùng bù với một góc thứ ba thì bằng nhau” là
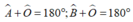
Chọn đáp án A
CÂU1: \(biết\) \(\widehat{xOy}\)\(=\)\(70^o\). \(Góc\) \(kề\) \(bù\) \(với\) \(\widehat{xOy}\) \(có\) \(số\) \(đo\) \(bằng\):
\(A.20^o\) \(B.70^o\) \(C.110^0\) \(D.180^o\)
Với 2 góc kề bù, ta có định lí sau: 2 tia phần giác của 2 góc kề bù tạo thành 1 góc vuông.
a. Hãy vẽ 2 góc xOy và yOx' kề bù, tia phân giác Ot của góc xOy, tia phân giác Ot' của góc yOx; và gọi số đo của góc xOy là m0
b. Hãy viết giả thiết và kết luận của định lí.
c. Hãy điền vào chỗ trống (...) và sắp xếp 4 câu sau đây 1 cách hợp lí để chứng minh định lí trên.
1) Góc tOy = \(\frac{1}{2}\)mo vì .....
2) Góc t'Oy = \(\frac{1}{2}\)( 180o - mo ) vì ........
3) Góc tOt' = 90o vì .......
4) Góc x'Oy = 180o - mo vì ......
Giúp mình với :)
Cho góc xOy. Điểm A thuộc Ox ; B thuộc Oy. Qua A vẽ đường thẳng a vuông góc với Ox ; qua B vẽ đường thẳng b vuông góc với Oy. CMR :
a) Nếu a cắt b thì xOy < 180o
b) Nếu a // b thì xOy = 180o
c) Nếu a | b thì xOy = 90o
1) Tam giác ABC vuông tại A, có góc B bằng 60o. CM là tia phân giác góc ACB. Tính số đo góc AMC
2) Cho \(\Delta ABC\)có AB<BC. Trên tia BA lấy điểm D sao cho BC=BD. Tia phân giác của góc B cắt cạnh AC ở E. Gọi K là trung điểm của DC.
a) Chứng minh: ED=EC
b) Chứng minh: \(EK\perp DC\)
Các bạn chỉ cần làm b) của 2) thôi nhé! Khỏi cần vẽ hình cũng đc. Mình đã làm đc 1) và a) của 2) rồi nên bạn nào lười chỉ cần làm phần b) giúp mình thôi nhé! Nếu có sai sót thì các bạn sửa giúp mình. Thanks!
1) Xét \(\Delta ABC\)có:
\(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^o\)
\(90^o+60^o+\widehat{ACB}=180^o\)
\(150^o+\widehat{ACB}=180^o\)
\(\widehat{ACB}=180^o-150^o\)
Vậy \(\widehat{ACB}=30^o\)
Mà CM là tia phân giác góc \(\widehat{ACB}\)nên:
\(\widehat{ACM}=\widehat{MCB}=\frac{\widehat{ACB}}{2}=\frac{30^o}{2}=15^o\)
Vậy \(\widehat{ACM}=\widehat{MCB}=15^o\)
Xét \(\Delta AMC\)có:
\(\widehat{BAC}+\widehat{AMC}+\widehat{ACM}=180^o\)
\(90^o+\widehat{AMC}+15^o=180^o\)
\(105^o+\widehat{AMC}=180^o\)
\(\widehat{AMC}=180^o-105^o\)
Vậy \(\widehat{AMC}=75^o\)
2) a) Xét \(\Delta ADE\)và \(\Delta CKE\) có:
AE=CE (E là tia phân giác cạnh AC)
\(\widehat{DEA}=\widehat{KEC}\) (đối đỉnh)
\(\widehat{C}\): Cạnh chung
Vậy \(\Delta ADE=\Delta CKE\) (g-c-g)
Suy ra: ED=EC (hai cạnh tương ứng)
b) Chứng minh: \(EK\perp DC\)
1. Tam giác DEF cân tại E, kết luận nào sau đây là đúng ?
A. E=F B. ED=EF C. DE=DF D. FE=FD
2. Tam giác ABC vuông tại C thì :
A. Â+B=180o B. B+C=90o C. A+B=90o D. A+C=90o
Tam giác ABC cân tại A có \(\widehat{A}\) \(=40^o\) thì góc ngoài tại đỉnh C bằng:
A. \(40^o\) B. \(90^o\) C. \(100^o\) D. \(110^o\)
Cho tam giác ABC có góc B bằng 50o. Trên tia đối của tia AB lấy điểm O. Trên nửa mp kong6 chứa C bờ AB vẽ xÔy=50o
a) Cmr: Ox//BC
b) Qua A vẽ d//BC, Cmr: góc ABC + góc BAC + góc ACB =180o
B1 , Cho hÌNH vẽ biêt góc BAD + ADC = 180o vÀ gÓC ADC = 90o .
a, CMR : AB song song CD
b, BC vuÔng góc CD
Ai nhang mik sẼ tick nha !!! Help me !!!!
Bài 3. Cho tam giác ABC có \(\widehat{BAC}=a\left(0^o< a< 180^o\right)\) , hai đường phân giác của góc B, C cắt nhau tại T. Tính theo \(\widehat{BTC}\) theo a. Tìm a biết \(\widehat{BTC}=2\times\widehat{BAC}\)
cho 2 góc O và I có cạnh tương ứng song song.Biết góc O+góc I=a độ(0<a<180).Hỏi xác định đc số đo của 2 góc O và I ko?