Các câu hỏi tương tự
Giả sử đồ thị của hàm số y f (x) là (C), khi tịnh tiến (C) theo Ox qua phải 1 đơn vị thì sẽ được đồ thị của hàm số:
Đọc tiếp
Giả sử đồ thị của hàm số y = f (x) là (C), khi tịnh tiến (C) theo Ox qua phải 1 đơn vị thì sẽ được đồ thị của hàm số:
![]()
![]()
![]()
![]()
Giả sử đồ thị của hàm số
y
x
4
-
2
x
2
-
1
là
C
, khi tịnh tiến
C
theo
O
y
lên trên 1 đơn vị thì sẽ được đồ thị của hàm số
Đọc tiếp
Giả sử đồ thị của hàm số y = x 4 - 2 x 2 - 1 là C , khi tịnh tiến C theo O y lên trên 1 đơn vị thì sẽ được đồ thị của hàm số
![]()
![]()
![]()
![]()
Giả sử đồ thị của hàm số
y
x
4
-
2
x
2
-
1
là
(
C
)
, khi tịnh tiến
(
C
)
theo
O
x
qua trái 1 đơn vị thì sẽ được đồ thị của một hàm số tr...
Đọc tiếp
Giả sử đồ thị của hàm số y = x 4 - 2 x 2 - 1 là ( C ) , khi tịnh tiến ( C ) theo O x qua trái 1 đơn vị thì sẽ được đồ thị của một hàm số trong 4 hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
![]()
![]()
![]()
![]()
Cho vectơ
v
→
a
;
b
sao cho khi tịnh tiến đồ thị hàm số
y
f
x
x
2
-
x
+
1
x
-
1
theo véc tơ...
Đọc tiếp
Cho vectơ v → = a ; b sao cho khi tịnh tiến đồ thị hàm số y = f x = x 2 - x + 1 x - 1 theo véc tơ v → ta nhận đồ thị hàm số y = g x = x 2 x + 1 . Khi đó tích a.b bằng
A. 1
B. 5
C. 6
D. 4
Giả sử F(x) là nguyên hàm của hàm số f(x)4x-1. Đồ thị hàm số F(x) và f(x) cắt nhau tại một điểm trên trục tung. Tọa độ các điểm chung của hai đồ thị hàm số trên là:
Đọc tiếp
Giả sử F(x) là nguyên hàm của hàm số f(x)=4x-1. Đồ thị hàm số F(x) và f(x) cắt nhau tại một điểm trên trục tung. Tọa độ các điểm chung của hai đồ thị hàm số trên là:
![]()
![]()
![]()
![]()
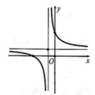
Hàm số yf(x) có đồ thị như hình vẽ bên. Hình nào dưới đây là đồ thị của hàm số y|f(x)| A. Hình 1 B. Hình 2 C. Hình 3 D. Hình 4
Đọc tiếp
Hàm số y=f(x) có đồ thị như hình vẽ bên. Hình nào dưới đây là đồ thị của hàm số y=|f(x)|
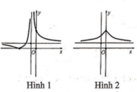
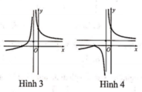
A. Hình 1
B. Hình 2
C. Hình 3
D. Hình 4
Cho hàm số
y
f
(
x
)
a
x
4
+
b
x
2
+
c
có đồ thị như hình bên dưới. Tìm tổng tất cả các đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
y
x
(
x
-
1
)
f...
Đọc tiếp
Cho hàm số
y
=
f
(
x
)
=
a
x
4
+
b
x
2
+
c
có đồ thị như hình bên dưới. Tìm tổng tất cả các đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
y
=
x
(
x
-
1
)
f
(
x
)
-
1
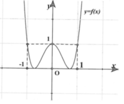
![]()
![]()
![]()
![]()
Cho hàm số y f(x) có đạo hàm trên R và đồ thị hình bên dưới là đồ thị của đạo hàm số : y f’(x) . Hàm số y g(x) f(x) + x đạt cực tiểu tại điểm A. x 0 B.x 1 C. x 2 D. Không có điểm cực tiểu
Đọc tiếp
Cho hàm số y= f(x) có đạo hàm trên R và đồ thị hình bên dưới là đồ thị của đạo hàm số : y= f’(x) . Hàm số y= g(x) = f(x) + x đạt cực tiểu tại điểm
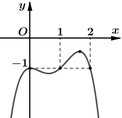
A. x= 0
B.x= 1
C. x= 2
D. Không có điểm cực tiểu
Cho hàm số y f(x) có đạo hàm trên R và đồ thị hình bên dưới là đồ thị của đạo hàm f’(x) . Hàm số nghịch biến trên khoảng A (-3 ; -2) B. (- 2 ; -1) C. (- 1 ; 0) D. (0 ; 2)
Đọc tiếp
Cho hàm số y= f(x) có đạo hàm trên R và đồ thị hình bên dưới là đồ thị của đạo hàm f’(x) .
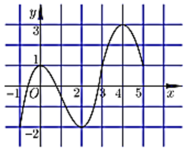
Hàm số ![]() nghịch biến trên khoảng
nghịch biến trên khoảng
A (-3 ; -2)
B. (- 2 ; -1)
C. (- 1 ; 0)
D. (0 ; 2)



