Các câu hỏi tương tự
Giả sử Bm là tập hợp các bội số của m (m≠0). Chứng minh Bn⊂ Bm khi và chỉ khi n là bội số của m.
Gọi z1, z2 là các nghiệm của phương trình
z
2
-
4
z
+
9
0
. Giả sử M, N là các điểm biểu diễn hình học của z1 và z2 trên mặt phẳng phức. Khi đó độ dài của MN là: A. 4 B. 5 C.
-
2
5
D.
2...
Đọc tiếp
Gọi z1, z2 là các nghiệm của phương trình z 2 - 4 z + 9 = 0 . Giả sử M, N là các điểm biểu diễn hình học của z1 và z2 trên mặt phẳng phức. Khi đó độ dài của MN là:
A. 4
B. 5
C. - 2 5
D. 2 5
Trong không gian Oxyz , cho ba mặt cầu lần lượt có phương trình là
(
x
+
5
)
2
+
(
y
-
1
)
2
+
z...
Đọc tiếp
Trong không gian Oxyz , cho ba mặt cầu lần lượt có phương trình là ( x + 5 ) 2 + ( y - 1 ) 2 + z 2 = 5 ; x 2 + ( y + 2 ) 2 + ( z - 3 ) 2 = 6 và ( x + 1 ) 2 + y 2 + ( z - 4 ) 2 = 9 . Gọi M là điểm di động ở ngoài ba mặt cầu và X, Y , Z là các tiếp điểm của các tiếp tuyến vẽ từ M đến ba mặt cầu. Giả sử MX = MY = MZ , khi đó tập hợp các điểm M là đường thẳng có vectơ chỉ phương là
![]()
![]()
![]()
![]()
Gọi S là tập hợp các nghiệm thuộc đoạn
−
2
π
;
2
π
của phương trình
5
sin
x
+
cos
3
x
+
sin
3
x...
Đọc tiếp
Gọi S là tập hợp các nghiệm thuộc đoạn − 2 π ; 2 π của phương trình 5 sin x + cos 3 x + sin 3 x 1 + 2 sin 2 x = cos 2 x + 3 .
Giả sử M,m là phần tử lớn nhất và nhỏ nhất của tập hợp S. Tính H = M-m.
A. H = 2 π .
B. H = 10 π 3 .
C. H = 11 π 3 .
D. H = 7 π 3 .
Cho hàm số
y
x
4
-
6
x
2
+
m
có đồ thị
C
m
.Giả sử
C
m
cắt trục hoành tại bốn điểm phân biệt sao cho hình phẳng giới hạn bởi
C
m
và trục hoành có phần phía trên trục hoành và phần phía dưới trục hoành có diện tích...
Đọc tiếp
Cho hàm số y = x 4 - 6 x 2 + m có đồ thị C m .Giả sử C m cắt trục hoành tại bốn điểm phân biệt sao cho hình phẳng giới hạn bởi C m và trục hoành có phần phía trên trục hoành và phần phía dưới trục hoành có diện tích bằng nhau. Khi đó m = a b (với a,b là các số nguyên, b > 0 ; a b là phân số tối giản). Giá trị của biểu thức S=a+b là:
A. 7.
B. 6.
C. 5.
D. 4.
Giả sử đồ thị (C) của hàm số
f
x
a
x
3
+
b
x
2
+
c
x
+
d
có hai điểm cực trị là
M
(
-
1
;
7
)
và
N
(
5
;
-
7
)
. Gọi
x
1
;
...
Đọc tiếp
Giả sử đồ thị (C) của hàm số f x = a x 3 + b x 2 + c x + d có hai điểm cực trị là M ( - 1 ; 7 ) và N ( 5 ; - 7 ) . Gọi x 1 ; x 2 ; x 3 là hoành độ giao điểm của (C) với trục hoành. Khi đó x 1 + x 2 + x 3 bằng
A. 6
B. 4
C. 3
D. 2
Cho K là tập hợp các số tự nhiên có bốn chữ số. Chọn ngẫu nhiên một số từ K. Tính xác suất để số được chọn có tổng các chữ số là bội của 4 .
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAB là tam giác vuông cân tại S và nằm trong mặt phẳng vuông góc vói đáy. Gọi M là trung điểm của SC và
α
là số đo của góc giữa hai đường thẳng AC, BM. Khi đó
cos
α
bằng
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAB là tam giác vuông cân tại S và nằm trong mặt phẳng vuông góc vói đáy. Gọi M là trung điểm của SC và α là số đo của góc giữa hai đường thẳng AC, BM. Khi đó cos α bằng
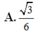
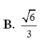

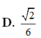
Tập hợp tất cả các giá trị thực của tham số m để hàm số
y
2
x
2
+
1
-
m
x
+
1
+...
Đọc tiếp
Tập hợp tất cả các giá trị thực của tham số m để hàm số y = 2 x 2 + 1 - m x + 1 + m x - m đồng biến trên 1 ; + ∞ là ( - ∞ ; a ] . Khi đó a thuộc khoảng nào ?
![]()
![]()
![]()
![]()



