Bài 2:
Gọi O là giao điểm hai đường chéo
Suy ra O vừa là trung điểm của AC và BD mà \(AC=BD\) ( tính chất trong hình chữ nhật)
\(\Rightarrow OA=OB=OC=OD=\dfrac{AC}{2}=\dfrac{\sqrt{AB^2+BC^2}}{2}=5\)
Vậy tâm đường tròn đi qua bốn điểm A,B,C,D là điểm O và có bán kính 5cm
Bài 1:
Gọi O là trung điểm của BC
\(\Leftrightarrow OB=OC=\dfrac{BC}{2}\)
Ta có \(OA=\dfrac{BC}{2}=\dfrac{\sqrt{9^2+12^2}}{2}=7,5cm\) ( tính chất đg trung tuyến ứng với cạnh huyền trong tam giác vuông)
\(\Rightarrow OA=OB=OC\)
Suy ra tâm đường tròn đi qua ba điểm A,B,C là điểm O và có bán kính \(R=7,5cm\)

 ghi rõ giúp e ạaa
ghi rõ giúp e ạaa


 giúp e với ạaa
giúp e với ạaa
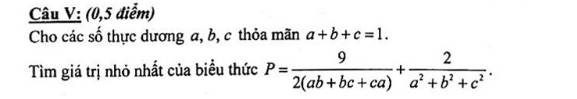 giúp e vs ạaa
giúp e vs ạaa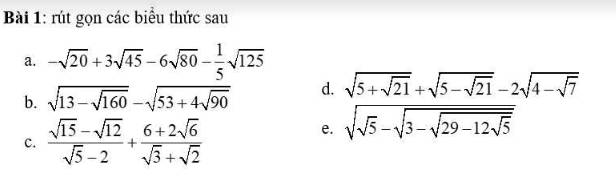 giúp e với ạaa
giúp e với ạaa giúp e gấp với ạaa
giúp e gấp với ạaa giúp e gấp với ạaa
giúp e gấp với ạaa



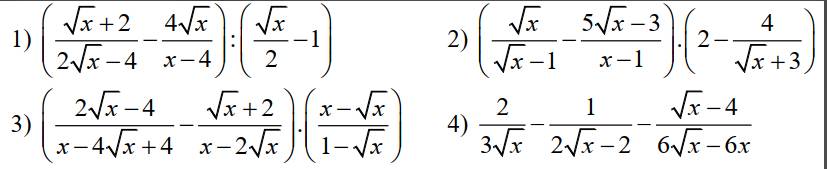 giúp e bài này với ạaa
giúp e bài này với ạaa