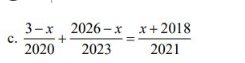\(\dfrac{3-x}{2020}+\dfrac{2026-x}{2023}=\dfrac{x+2018}{2021}\\ =>\dfrac{3-x}{2020}+\left(\dfrac{2026-x}{2023}-1\right)=\dfrac{x+2018}{2021}-1\\ =>\dfrac{3-x}{2020}+\dfrac{3-x}{2023}=\dfrac{x-3}{2021}\\ =>\dfrac{x-3}{2021}+\dfrac{x-3}{2020}+\dfrac{x-3}{2023}=0\\ =>\left(x-3\right)\left(\dfrac{1}{2021}+\dfrac{1}{2020}+\dfrac{1}{2023}\right)=0\\ =>x-3=0\\ =>x=3\)
A ¹/5 x 6 +1/6x7+.....+1/17x15
Gấp gấp gấp gấp gấp gấp
tìm các số tự nhiên x,y biết
59xy chia hết cho 9 và x-y=3
(59xy có gạch đầu nha, nhưng mình ko biết viết như thế nào nên viết đỡ, các bạn thông cảm)
cho mình cách giải luôn nha
mình đang cần GẤP GẤP GẤP GẤP GẤP GẤP GẤP GẤP GẤP GẤP GẤP
CỨU VỚI: ĐỀ THI HSG NĂM 2015 - 2016 CỦA PHÒNG GIÁO DỤC ĐÀO TẠO HỘI AN
Bài 2:
a) Tìm số dư của phép chia \(2^{2016}cho1+2+2^2+2^3+...+2^{2012}\)
NHỚ GHI LỜI GIẢI NHÉ!!!!!!!!!!!!!!!!!
cứu với gấp lắm
cứu với gấp lắm
cứu với gấp lắm
cứu với gấp lắm
cứu với gấp lắm
cứu với gấp lắm
cứu với gấp lắm
cứu với gấp lắm
cứu với gấp lắm
cứu với gấp lắm
cứu với gấp lắm
cứu với gấp lắm
cứu với gấp lắm
cứu với gấp lắm
cứu với gấp lắm
cứu với gấp lắm
cứu với gấp lắm
cứu với gấp lắm
cứu với gấp lắm
cứu với gấp lắm
cứu với gấp lắm
cứu với gấp lắm
cứu với gấp lắm
cứu với gấp lắm
cứu với gấp lắm
tìm 2 chữ số cuối cùng bên phải của số 7 mũ 2009
ghi cách giải giùm mình nha'
THANKS
MÌNH ĐANG CẦN GẤP GẤP GẤP GẤP GẤP GẤP LẮM LẮM LẮM LẮM LẮM
Giải giúp mik với,trình bày chi tiết giúp mik nha
Gấp,gấp,gấp....
Cho hỏi:
864.48-432.96/864.48.432=? Tính nhanh
Gấp gấp gấp!
tìm 2 số biết :
a . tổng của chúng gấp 9 lần hiệu của chúng và tích gấp 80 lần hiệu
b . tổng của chúng gấp 3 lần hiệu và tích gấp 18 lần hiệu
gấp :((
gấp gấp
TÌm số tự nhiên lớn nhất khi chia cho 3,5,9 dư lần lượt là 2,3,5
Gấp!Gấp!Gấp!
2-x-2=1024
x bằng bao nhiu
làm ơn nha gấp gấp gấp gấp lắm . ai trả lời đúng đầu tiên thì mình tick
