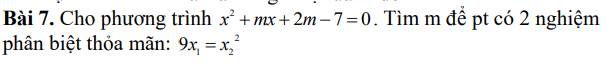\(\Delta=m^2-4\left(2m-7\right)=\left(m-4\right)^2+12>0;\forall m\)
Pt luôn có 2 nghiệm pb với mọi m
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-m\\x_1x_2=2m-7\end{matrix}\right.\)
Do \(x_2\) là nghiệm nên:
\(x_2^2+mx_2+2m-7=0\Rightarrow x_2^2=-mx_2-2m+7\)
Thế vào ta được:
\(9x_1=x_2^2=-mx_2-2m+7\)
\(\Rightarrow9\left(-m-x_2\right)=-mx_2-2m+7\)
\(\Rightarrow\left(m-9\right)x_2=7m+7\)
\(\Rightarrow x_2=\dfrac{7m+7}{m-9}\) (\(m\ne9\))
\(\Rightarrow x_1=-m-x_2=\dfrac{-m^2+2m-7}{m-9}\)
Thế vào \(x_1x_2=2m-7\)
\(\Rightarrow\left(\dfrac{-m^2+2m-7}{m-9}\right)\left(\dfrac{7m+7}{m-9}\right)=2m-7\)
\(\Rightarrow9m^3-50m^2+323m-518=0\)
\(\Rightarrow\left(m-2\right)\left(9m^2-32m+259\right)=0\)
\(\Rightarrow m=2\)