\(\left\{{}\begin{matrix}x^2y+xy^2=30\\x^3+y^3=35\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xy\left(x+y\right)=30\\\left(x+y\right)^3-3xy\left(x+y\right)=35\end{matrix}\right.\)
Đặt: \(\left\{{}\begin{matrix}x+y=S\\xy=P\end{matrix}\right.\) ta có:
\(\left\{{}\begin{matrix}PS=30\\S^3-3PS=35\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}PS=30\\S^3-3\cdot30=35\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}PS=30\\S^3=125\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}PS=30\\S=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}P=\dfrac{30}{5}=6\\S=5\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}xy=6\\x+y=5\end{matrix}\right.\)
Khi đó x và y là nghiệm của pt:
\(t^2-5t+6=0\)
\(\Delta=\left(-5\right)^2-4\cdot1\cdot6=1>0\)
\(t_1=\dfrac{5+\sqrt{1}}{2}=3\)
\(t_2=\dfrac{5-\sqrt{1}}{2}=2\)
Vậy: \(\left(x;y\right)=\left\{\left(2;3\right);\left(3;2\right)\right\}\)
\(\left\{{}\begin{matrix}x+y+xy=11\\x^2y+xy^2=30\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x+y\right)+xy=11\\xy\left(x+y\right)=30\end{matrix}\right.\)
Đặt: \(\left\{{}\begin{matrix}x+y=S\\xy=P\end{matrix}\right.\)
\(\left\{{}\begin{matrix}S+P=11\\PS=30\end{matrix}\right.\)
Khi đó S và P là nghiệm của pt:
\(t^2-11t+30=0\)
\(\Delta=\left(-11\right)^2-4\cdot1\cdot30=1>0\)
\(t_1=\dfrac{11+\sqrt{1}}{2}=6\)
\(t_2=\dfrac{11-\sqrt{1}}{2}=5\)
TH1: \(\left\{{}\begin{matrix}P=5\\S=6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xy=5\\x+y=6\end{matrix}\right.\)
Khi đó x và y là nghiệm của pt:
\(t^2-6x+5=0\)
\(\Rightarrow\left(x;y\right)=\left\{\left(1;5\right);\left(5;1\right)\right\}\)
TH2: \(\left\{{}\begin{matrix}P=6\\S=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xy=5\\x+y=6\end{matrix}\right.\)
Khi đó x và y là nghiệm của pt:
\(t^2-6x+5=0\)
\(\Rightarrow\left(x;y\right)=\left\{\left(3;2\right);\left(2;3\right)\right\}\)
Vậy: \(\left(x;y\right)=\left\{\left(1;5\right);\left(5;1\right);\left(2;3\right);\left(3;2\right)\right\}\)

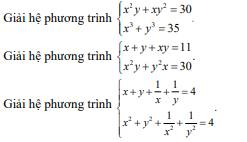 gấp
gấp