c: CE*CA=CF*CB
=>\(\dfrac{CE}{CB}=\dfrac{CF}{CA}\)
Xét ΔCEF vuông tại C và ΔCBA vuông tại C có
\(\dfrac{CE}{CB}=\dfrac{CF}{CA}\)
Do đó: ΔCEF đồng dạng với ΔCBA
=>\(\dfrac{S_{CBA}}{S_{CEF}}=\left(\dfrac{AB}{EF}\right)^2=\left(\dfrac{AB}{CH}\right)^2\)
\(\dfrac{1}{sin^2CAB}+\dfrac{1}{cos^2HCB}\)
\(=\dfrac{1}{sin^2CAB}+\dfrac{1}{cos^2CAB}\)
\(=\dfrac{cos^2CAB+sin^2CAB}{\left(sinCAB\cdot cosCAB\right)^2}=\dfrac{1}{\left(\dfrac{CB}{BA}\cdot\dfrac{CA}{BA}\right)^2}\)
\(=\dfrac{1}{\left(\dfrac{CH\cdot AB}{AB^2}\right)^2}=\dfrac{1}{\left(\dfrac{CH}{AB}\right)^2}=\dfrac{AB^2}{CH^2}\)
=>\(\dfrac{S_{CBA}}{S_{CEF}}=\dfrac{1}{sin^2CAB}+\dfrac{1}{cos^2HCB}\)(ĐPCM)


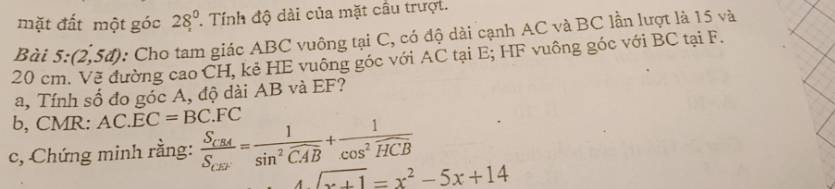 gấp phần c mn ơi
gấp phần c mn ơi





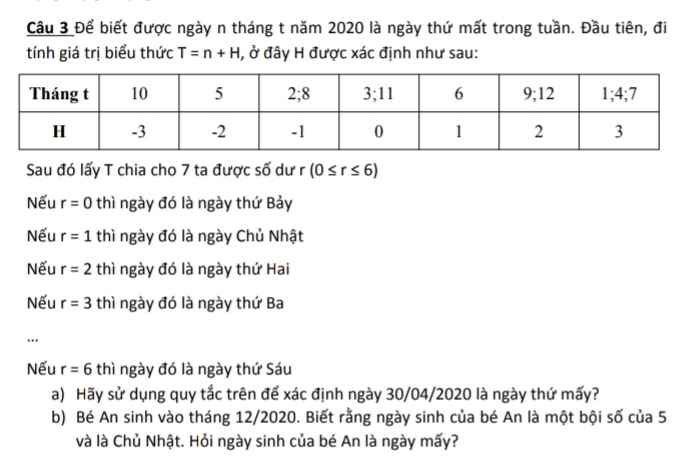





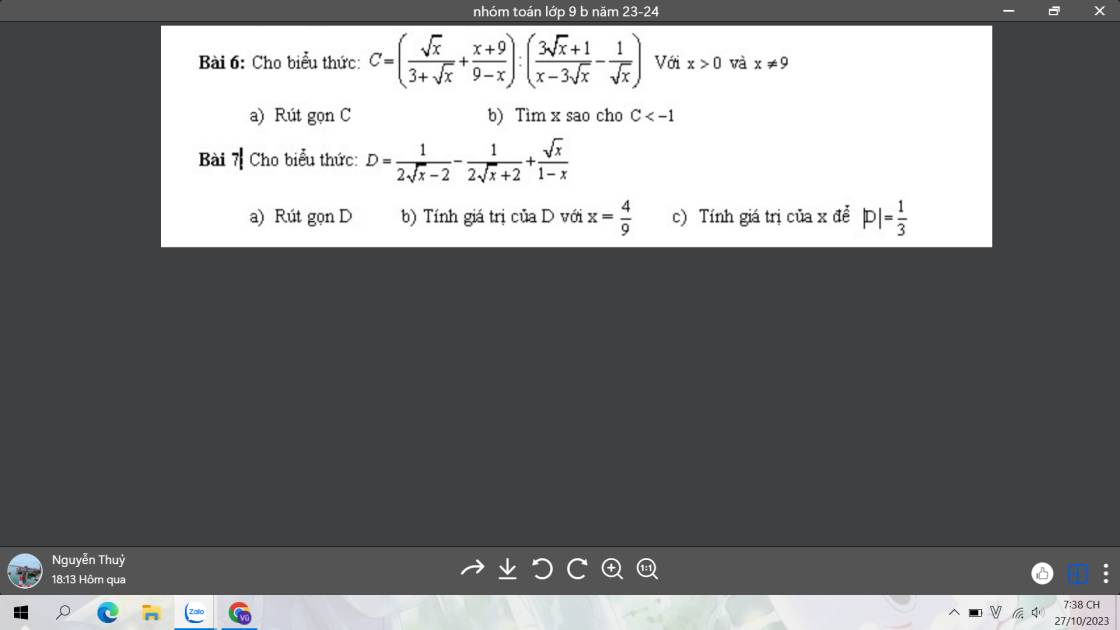 giúp mik với mn ơi mik đg cần gấp
giúp mik với mn ơi mik đg cần gấp


 mn ơi help mình viowis ạ mình đang cần gấp plssssssss
mn ơi help mình viowis ạ mình đang cần gấp plssssssss


