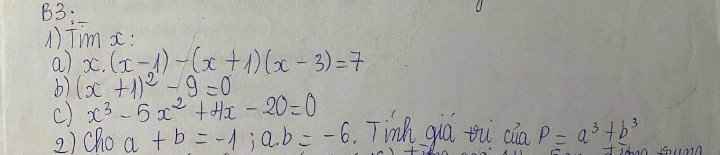\(1,\\ a,\Rightarrow x^2-x-x^2+2x+3=7\\ \Rightarrow x=4\\ b,\Rightarrow\left(x+1\right)^2=9\Rightarrow\left[{}\begin{matrix}x+1=3\\x+1=-3\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=2\\x=-4\end{matrix}\right.\\ c,\Rightarrow x^2\left(x-5\right)+4\left(x-5\right)=0\\ \Rightarrow\left(x^2+4\right)\left(x-5\right)=0\\ \Rightarrow\left[{}\begin{matrix}x^2=-4\left(vô.lí\right)\\x=5\end{matrix}\right.\Rightarrow x=5\\ 2,\\ a^3+b^3=\left(a+b\right)^3-3ab\left(a+b\right)\\ =\left(-1\right)^3-3\left(-1\right)\left(-6\right)=-1-18=-19\)
Đúng 2
Bình luận (0)
Các câu hỏi tương tự
Một tập hợp có 5 số nguyên dương có trung bình cộng là 5, trung vị cũng là 5 và có mode duy nhất là 8. Hỏi hiệu số lớn nhất của số lớn nhất và số bé nhất của tập hơn số trên là bao nhiêu?giúp mik , mik cần gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp lắm
Đọc tiếp
Một tập hợp có 5 số nguyên dương có trung bình cộng là 5, trung vị cũng là 5 và có mode duy nhất là 8. Hỏi hiệu số lớn nhất của số lớn nhất và số bé nhất của tập hơn số trên là bao nhiêu?
giúp mik , mik cần gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp gấp lắm
GẤP, GẤP, GẤP, MÌNH ĐANG CẦN GẤP LẮM, LÀM ƠN GIÚP MÌNH VỚI
Gấp gấp
Gấp gấp ạ
Giúp em với gấp rất gấp 
Ai làm giúp em với gấp gấp
hãy tìm các hình mà khi gấp đôi nó lại sẽ chia được thành hai phần bằng nhau
và cái mép gấp đó được gọi là gì (gấp theo hai cách )(cách 1 gấp theo chiều rồng và ngược lại với cách 2)
Cho a,b,c thoả mãn:
a^2/b+c +b^2/c+a
+c^2/a+b =3 và a/b+c +b/c+a +c/a+b =2
Tính giá trị của P=a+b+c
Cần gấp gấp gấp.....gấp lắm. Mọi người giải giúp mình nha
Hỏi gấp hỏi gấp
Sắt và sắt gỉ cái nào nặng hơn???