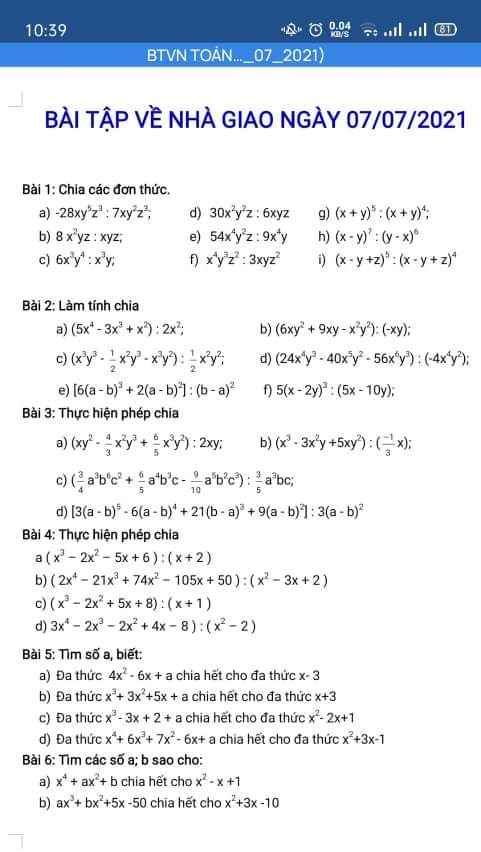Câu 16:
a: Xét tứ giác AMCK có
I là trung điểm chung của AC và MK
=>AMCK là hình bình hành
Hình bình hành AMCK có \(\widehat{AMC}=90^0\)
nên AMCK là hình chữ nhật
b: Ta có: ΔABC cân tại A
mà AM là đường cao
nên M là trung điểm của BC
AMCK là hình chữ nhật
=>AK//MC và AK=MC
Ta có: AK//MC
=>AK//MB
Ta có: AK=MC
MC=MB
Do đó: AK=MB
Xét tứ giác ABMK có
AK//MB
AK=MB
Do đó: ABMK là hình bình hành
c: Để AMCK là hình vuông thì AM=CM
=>AM=BC/2
Xét ΔABC có
AM là đường trung tuyến
BC=2AM
Do đó: ΔABC vuông tại A
=>\(\widehat{BAC}=90^0\)
Câu 2:
a: \(2\left(x-3\right)-4x=0\)
=>2x-6-4x=0
=>-2x-6=0
=>x+3=0
=>x=-3
b: \(2x\left(2x+2\right)-4x\left(x-2\right)=12\)
=>\(4x^2+4x-4x^2+8x=12\)
=>12x=12
=>\(x=\dfrac{12}{12}=1\)
c: \(x^2-2x+1=25\)
=>\(\left(x-1\right)^2=25\)
=>\(\left[{}\begin{matrix}x-1=5\\x-1=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5+1=6\\x=-5+1=-4\end{matrix}\right.\)










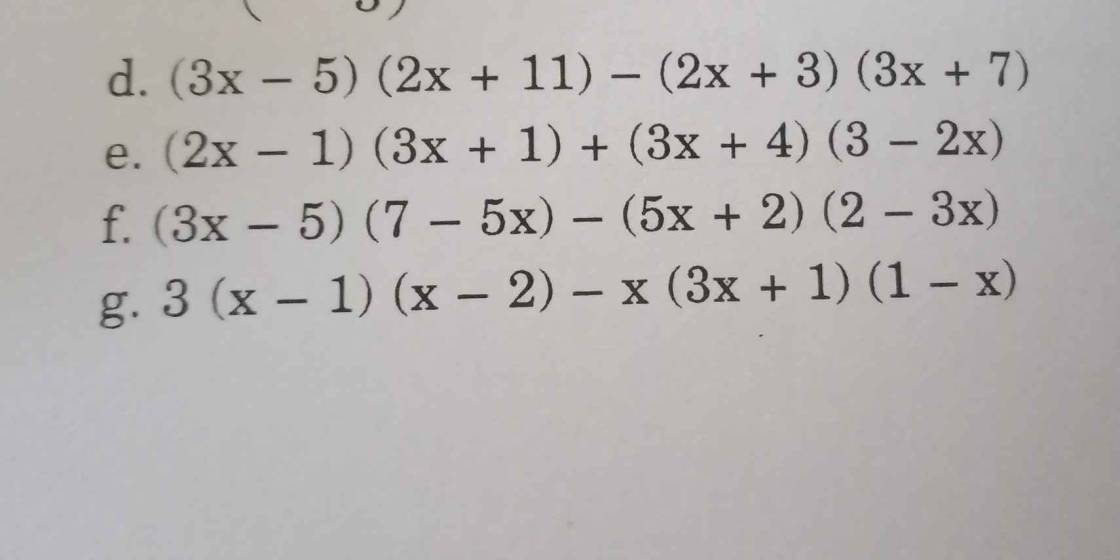


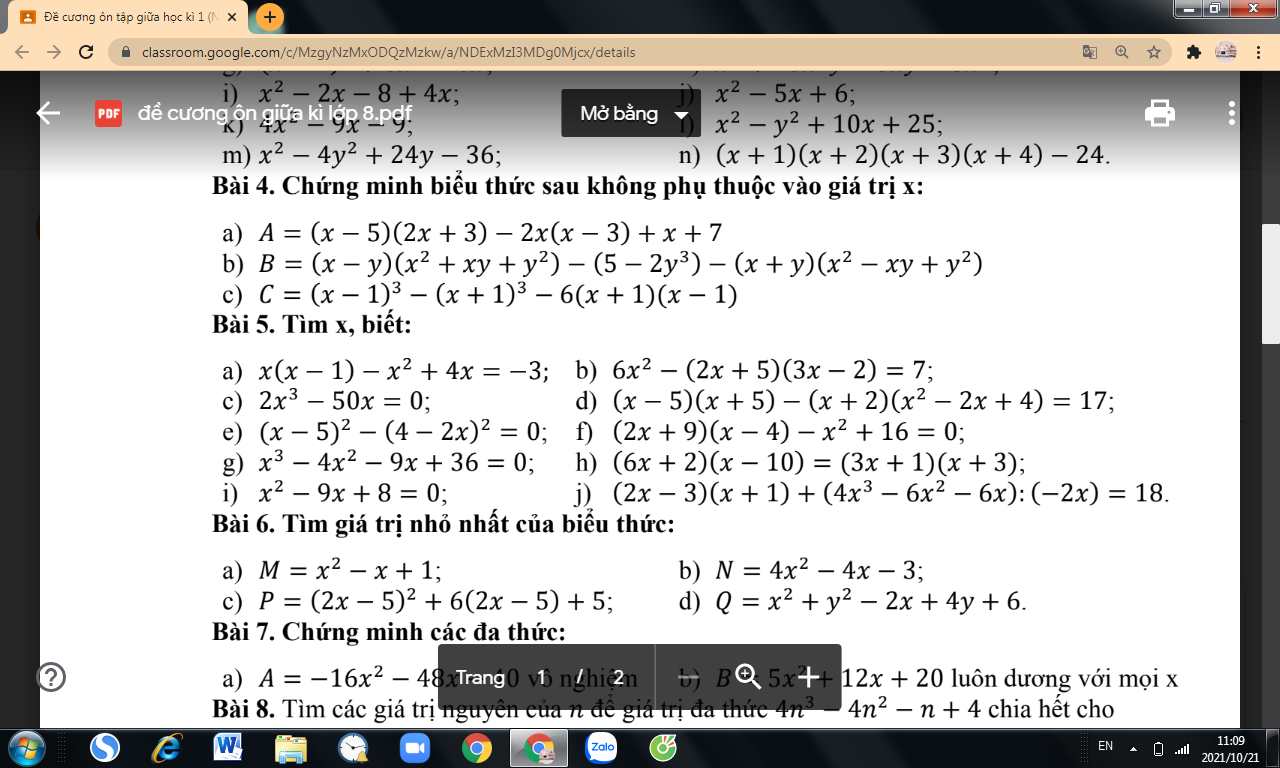

 Các bạn giúp mk giải ý f, g vs ạ
Các bạn giúp mk giải ý f, g vs ạ