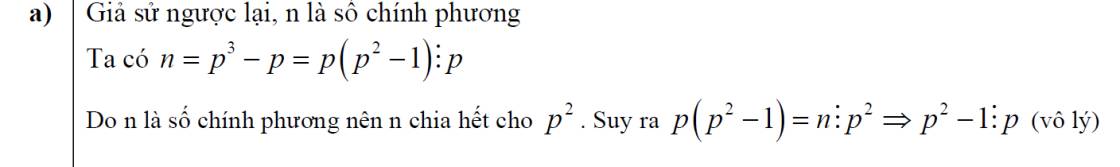Question

Em hơi cấn cái phần giải thích này mong được giải thích dễ hiểu hơn ạ

Answer 1

Lời giải:

Giả sử $n$ là số chính phương. Đặt $n=a^2$ với $a$ tự nhiên.

$a^2=n=p^3-p=p(p^2-1)\vdots p$

$\Rightarrow a\vdots p$ (do $p$ là số nguyên tố)

$\Rightarrow n=a^2\vdots p^2$

$\Rightarrow p(p^2-1)\vdots p^2$

$\Rightarrow p^2-1\vdots p$ (điều này vô lý vì hiển nhiên $gcd(p^2-1,p)=1$)

Vậy điều giả sử là sai. Tức là $n$ không thể là scp.