1.
a.
Do M là trung điểm AB, K là trung điểm AD nên \(\left\{{}\begin{matrix}AM=BM=\dfrac{1}{2}AB\\AK=DK=\dfrac{1}{2}AD\end{matrix}\right.\) (1)
Do N là trung điểm BC, I là trung điểm CD nên: \(\left\{{}\begin{matrix}BN=CN=\dfrac{1}{2}BC\\CI=DI=\dfrac{1}{2}CD\end{matrix}\right.\) (2)
Mà ABCD là hình bình hành nên: \(\left\{{}\begin{matrix}AB=CD\\AD=BC\\\widehat{A}=\widehat{C}\\\widehat{B}=\widehat{D}\end{matrix}\right.\) (3)
(1);(2);(3) \(\Rightarrow\left\{{}\begin{matrix}AM=CI\\AK=CN\\BM=DI\\BN=DK\end{matrix}\right.\)
Xét hai tam giác AKM và CIN có:
\(\left\{{}\begin{matrix}AM=CI\left(cmt\right)\\\widehat{A}=\widehat{C}\\AK=CN\left(cmt\right)\end{matrix}\right.\) \(\Rightarrow\Delta AKM=\Delta CIN\left(c.g.c\right)\)
Xét hai tam giác BMN và DIK có:
\(\left\{{}\begin{matrix}BM=DI\left(cmt\right)\\\widehat{B}=\widehat{D}\\BN=DK\end{matrix}\right.\) \(\Rightarrow\Delta BMN=\Delta DIK\left(c.g.c\right)\)
b.
Do \(\Delta AKM=\Delta CIN\Rightarrow KM=IN\) (4)
Do \(\Delta BMN=\Delta DIK\Rightarrow MN=IK\) (5)
(4);(5) \(\Rightarrow MNIK\) là hình bình hành
c.
Do \(AM=CI\left(cmt\right)\), mà \(AB||CD\Rightarrow AM||CI\)
\(\Rightarrow AMCI\) là hình bình hành (tứ giác có cặp cạnh đối song song và bằng nhau)
\(\Rightarrow\) Hai đường chéo AC, MI cắt nhau tại trung điểm mỗi đường
Mà O là trung điểm MI \(\Rightarrow O\) là trung điểm AC
2.
Cho ABCD là hình bình hành, mà \(AB=BC\)
\(\Rightarrow ABCD\) là hình thoi
Mà AC, BD là các đường chéo của hình thoi ABCD nên:
a.
Theo tính chất hình thoi, ta có BD là phân giác góc B và AC là phân giác góc A
b.
Theo tính chất hình thoi, ta có \(AC\perp BD\)




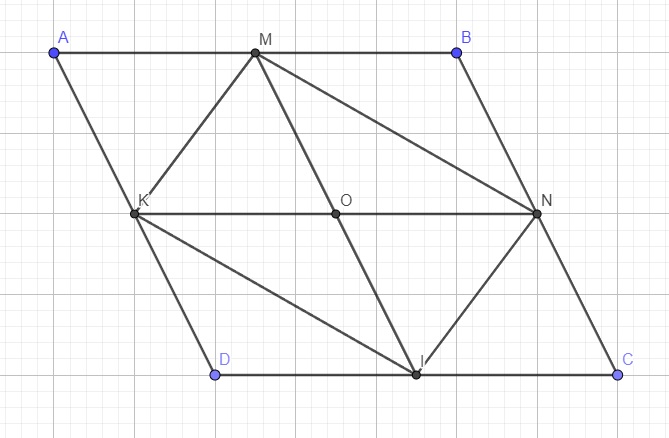


 Giúp e bài 2 thôi ạ bài 1 e làm r ạ! Mong mn giúp e, e cần gấp ạ!
Giúp e bài 2 thôi ạ bài 1 e làm r ạ! Mong mn giúp e, e cần gấp ạ!










