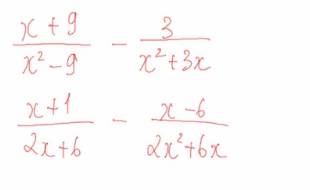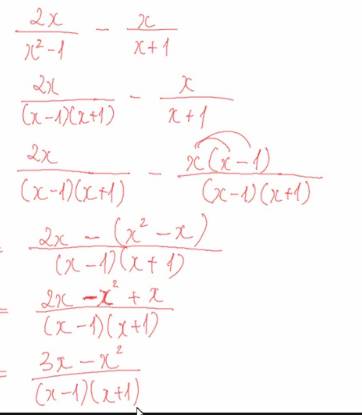Lời giải:
Hàm số bậc nhất là hàm có dạng $y=ax+b$ với $a,b$ là số thực, $a\neq 0$
Tất cả những hình thức của hàm số không đảm bảo điều kiện trên thì không phải hàm bậc nhất. Do đó nếu xuất hiện $x^2,x^3, \frac{1}{x},...$ thì hệ số gắn với nó phải bằng $0$.
-----------------
a.
Để hàm bậc nhất thì $m-1\neq 0\Leftrightarrow m\neq 1$
b.
Để hàm bậc nhất thì $m^2-4m+4\neq 0$
$\Leftrightarrow (m-2)^2\neq 0\Leftrightarrow m\neq 2$
c.
Để hàm bậc nhất thì $m-3\neq 0$ và $\frac{m+3}{m-3}\neq 0$
$\Leftrightarrow m\neq \pm 3$
d.
Để hàm bậc nhất thì:
\(\left\{\begin{matrix}\\
m^2-1=0\\
m^2-2m+1\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}\\
(m-1)(m+1)=0\\
(m-1)^2\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}\\
(m-1)(m+1)=0\\
m-1\neq 0\end{matrix}\right.\Leftrightarrow m+1=0\Leftrightarrow m=-1\)