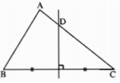
Ta có AC = AD + DC = AD + BD = 3,2 + 11,4 = 14,6 (cm).
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Đường trung trực của cạnh BC trong tam giác ABC cắt cạnh AC tại D. Hãy tìm: AD và CD nếu BD = 5cm; AC = 8cm
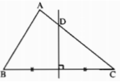
Đường trung trực của cạnh BC trong tam giác ABC cắt cạnh AC tại D. Cho AC = 10cm, BD = 4cm. Khi đó AD là:
A. 6cm
B. 4cm
C. 3cm
D. 5cm
Cho tam giác ABC vuông tại A, có góc ABC = 60*. Trên tia BC lấy điểm D sao cho BD = BA. Đường thẳng vuông góc với BC tại D cắt cạnh AC tại E, cắt tia BA tại F.
a) Tính số đo góc ACB và so sánh độ dài các cạnh của tam giác ABC.
b) Chứng minh: BE là đường trung trực của đoạn thẳng AD và BE là tia phân giác của góc ABC.
c) Chúng minh: AD // FC.
d) Chứng minh: AC = 3DE.
cho tam giác ABC vuông tại A coa AB=AC=5cm đường phân giác BD(D thuộc AC ) . kẻ DH vuông góc với BC tại H .a) tính độ dài cạnh BC b) chứng minh tam giác ABD = tam giác HBD và BD là đường trung trực của AH c) trên cạnh AB lấy E sao cho AC=AD . đường vuông góc với BD kẻ từ E cắt BC ở G . chứng minh GH=HC
Cho tam giác ABC vuông tại A có AC 6 cm, BC 10cm.
a) Tính độ dài cạnh AB và so sánh các góc của tam giác ABC.
b) Trên tia đối của tia AC lấy điểm D sao cho AD AC. Gọi K là trung điểm của cạnh BC, đường thẳng DK cắt cạnh AB tại M. Chứng minh BC BD và tính độ
dài đoạn thẳng AM.
c) Đường trung trực (d) của đoạn thẳng AB cắt đường thẳng DB tại Q. Chứng minh ba điểm C, M, Q thẳng hàng
Giúp mình bài này với
Mình cảm ơn trước nha
Đọc tiếp
Cho tam giác ABC vuông tại A có AC = 6 cm, BC = 10cm.
a) Tính độ dài cạnh AB và so sánh các góc của tam giác ABC.
b) Trên tia đối của tia AC lấy điểm D sao cho AD = AC. Gọi K là trung điểm của cạnh BC, đường thẳng DK cắt cạnh AB tại M. Chứng minh BC = BD và tính độ
dài đoạn thẳng AM.
c) Đường trung trực (d) của đoạn thẳng AB cắt đường thẳng DB tại Q. Chứng minh ba điểm C, M, Q thẳng hàng
Giúp mình bài này với
Mình cảm ơn trước nha
cho tam giác ABC .Lấy D thuộc cạnh AB,E thuộc cạnh AC sao cho BD=CE .Đường trung trực của đoạn thẳng BC cắt đường trung trực của đoạn thẳng DE tại điểm O.Chứng minh góc DAE=gócDOE
Cho tam giác ABC cân tại A. Các đường trung trực của AB và AC cắt nhau tại O. Lấy điểm D thuộc cạnh AB, điểm E thuộc cạnh AC sao cho BD CE. Chứng minh:a)
∆
D
O
B
∆
E
O
C
;
b) AO là đường trung trực của DE;c) DE // BC.
Đọc tiếp
Cho tam giác ABC cân tại A. Các đường trung trực của AB và AC cắt nhau tại O. Lấy điểm D thuộc cạnh AB, điểm E thuộc cạnh AC sao cho BD = CE. Chứng minh:
a) ∆ D O B = ∆ E O C ;
b) AO là đường trung trực của DE;
c) DE // BC.
Cho tam giác ABC cân tại A, trung trực của cạnh AC cắt CB tại điểm D (D nằm ngoài đoạn BC). Trên tia đối AD lấy E sao cho AE = BD. Chứng minh tam giác DCE cân
Cha tam giác ABC (AB<AC). Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho BD=CE. Các đường trung trực của BC và DE cắt nhau tại O. Chứng minh tam giác BOD = tam giác COE