Chọn C.
Phương trình tham số của đường thẳng đi qua M(2;1) nhận 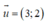 làm VTCP là:
làm VTCP là:
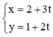
Chọn C.
Phương trình tham số của đường thẳng đi qua M(2;1) nhận 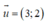 làm VTCP là:
làm VTCP là:
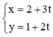
Đường thẳng đi qua M(3; 2) và nhận vectơ n → = 2 ; 1 làm vectơ pháp tuyến có phương trình tổng quát là:
A. 2x + y - 4 = 0
B. 2x + y - 8 = 0
C. x - 2y + 4 = 0
D. -2x + y - 8 = 0
Trong mặt phẳng Oxy, cho điểm A(2;-4), đường thẳng Δ: x = -3 + 2t, y = 1 + t và đường tròn (C): x^2 + y^2 – 2x – 8y – 8 = 0.
a. Tìm một vectơ pháp tuyến n của đường thẳng Δ. Lập phương trình tổng quát của đường thẳng d, biết d đi qua điểm A và nhận n làm vectơ pháp tuyến.
b. Viết phương trình đường tròn (T), biết (T) có tâm A và tiếp xúc với Δ.
c. Gọi P, Q là các giao điểm của Δ và (C). Tìm toạ độ điểm M thuộc (C) sao cho tam giác MPQ cân tại M.
cho đường thẳng d có phương trình x=1-4t y=-3+t. Một vectơ chỉ phương của d là A. vectơ u=(1;-4) B.vectơ u=(4;1) C.vectơ u=(1;-3) D.vectơ u=(-4;1)
Viết phương trình chính tắc của đường thẳng D đi qua M( -2; -1) và nhận vectơ u → ( 1 ; 2 ) làm vectơ chỉ phương.
A. 2x- y+ 3= 0
B. x + 2 1 = y + 1 2
C. x = - 2 + 1 t y = - 1 + 2 t
D: x - 1 - 2 = y - 2 - 1
Đường thẳng d đi qua điểm M (1; -2) và có vectơ chỉ phương u → = 3 ; 5 có phương trình tham số là:
A. d : x = 3 + t y = 5 − 2 t
B. d : x = 1 + 3 t y = − 2 + 5 t
C. d : x = 1 + 5 t y = − 2 − 3 t
D. d : x = 3 + 2 t y = 5 + t
Viết phương trình tham số của đường thẳng D đi qua M(2; 8) và nhận vectơ n → ( 1 ; 2 ) làm vectơ pháp tuyến.
A. x+ 2y= 18
B . x = 2 + t y = 8 + 2 t
C. x = 2 - 2 t y = 8 + t
D. x = 1 + 2 t y = 2 + 8 t
Phương trình tham số của đường thẳng ∆ đi qua điểm M(3; 4) và có vectơ chỉ phương là u → = 3 ; 4 là:
A. x = 1 + 3 t y = − 2 + 4 t
B. x = 3 + 3 t y = 4 + 4 t
C. x = 3 + 4 t y = 1 − 2 t
D. x = − 3 + t y = − 4 − 2 t
Viết phương trình đường thẳng (△):
a) đi qua M(1;2), vtcp u=(3;-4)
b) đi qua M(-2;4), vtpt n=(2;3)
c) đi qua 2 điểm A(-2;1); B(3;2)
d) đi qua M(4;-2), song song d: 3x-5y+7=0
e) đi qua N(1;-3), song song d: \(\left\{{}\begin{matrix}x-1-3t\\y=2+t\end{matrix}\right.\)
f) đi qua P(3;5), vuông góc (d): 2x-7y-1=0
g) đi qua Q(-2;0), vuông góc (d): \(\left\{{}\begin{matrix}x=2+5t\\y=1-t\end{matrix}\right.\)
h) đi qua I(1;-1) và tạo (d): x-3y+7=0 một góc α=\(\dfrac{\sqrt{2}}{10}\)
l) đi qua J(1;-1) và cách điểm K(2;3) một khoảng là \(\dfrac{19}{5}\)
Phương trình tham số của đường thẳng Δ đi qua M(1;-3) và nhận vectơ n → 1 ; 2 làm vectơ pháp tuyến.
A. ∆ : x + 2 y + 5 = 0
B. ∆ : x = 1 + t y = - 3 + 2 t
C. ∆ : x = 1 - 2 t y = - 3 + t
D. ∆ : x - 1 - 2 = y + 3 1