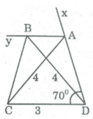
Phân tích: Giả sử hình thang ABCD dựng được thỏa điều kiện bài toán, ta thấy ΔACD xác định được vì biết CD = 3cm, ∠D = 70o, AC = 4cm
Ta cần xác định đỉnh B. Đỉnh B thỏa mãn 2 điều kiện:
- Nằm trên tia Ay//CD
- B cách D một khoảng bằng 4cm.
Cách dựng:
- Dựng đoạn CD = 3cm
- Dựng góc CDx bằng 70 0
- Trên nửa mặt phẳng bờ CD chứa tia Dx dựng cung tròn tâm C bán kính 4cm cắt Dx tại A.
- Dựng tia Ay // CD
- Trên nửa mặt phẳng bờ CD chứa điểm A, dựng cung tròn tâm D bán kính 4cm cắt Ay tại B
- Nối BC ta có hình thang ABCD cần dựng.
Chứng minh: Thật vậy theo cách dựng, ta có AB // CD nên tứ giác ABCD là hình thang có CD = 3cm , ∠ D = 70 0 , AC = 4cm.
Vậy ABCD là hình thang cân.
Biện luận: ∆ ACD luôn dựng được nên hình thang ABCD luôn dựng được.
Bài toán có một nghiệm hình.






