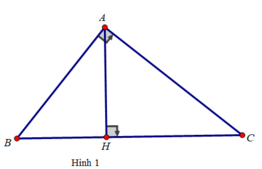
Các câu hỏi tương tự
a) Trong hình 44, hệ thức nào trong các hệ thức sau là đúng?
(
A
)
sin
α
b
c
(
B
)
cotg
α
b
c
(...
Đọc tiếp
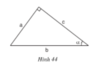
a) Trong hình 44, hệ thức nào trong các hệ thức sau là đúng?
( A ) sin α = b c ( B ) cotg α = b c ( C ) tg α = a c ( D ) cotg α = a c
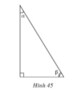
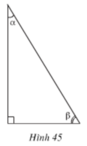
b) Trog hình 45, hệ thức nào trong các hệ thức sau không đúng ?
(A) sin2α + cos2α = 1
(B) sin α = cos β
(C) cos β = sin ( 90 ° – α )
(D) tg α = sin α cos α
Cho hình vẽ dưới.Hệ thứ nào dưới đây đúng? A.ca sin B B. ca có C C. ca sin C D. ca tan C giúp tui giải bài trên vs tui c.ơn
Đọc tiếp
Cho hình vẽ dưới.Hệ thứ nào dưới đây đúng?
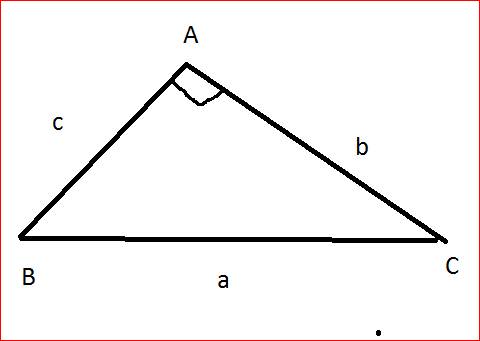
A.c=a sin B B. c=a có C C. c=a sin C D. c=a tan C
giúp tui giải bài trên vs ![]()
![]() tui c.ơn
tui c.ơn
Trog hình 45, hệ thức nào trong các hệ thức sau không đúng ? (A) sin2α + cos2α 1 (B) sin α cos β (C) cos β sin (90o – α)
D
t
g
α
sin
α
cos
α
Đọc tiếp
Trog hình 45, hệ thức nào trong các hệ thức sau không đúng ?
(A) sin2α + cos2α = 1
(B) sin α = cos β
(C) cos β = sin (90o – α)
D t g α = sin α cos α
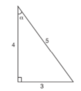
Chọn kết quả đúng trong các kết quả dưới đây:a) Trong hình 41, sin α bằng:
(
A
)
5
3
(
B
)
5
4
(
C
)
3
5...
Đọc tiếp
Chọn kết quả đúng trong các kết quả dưới đây:
a) Trong hình 41, sin α bằng:
( A ) 5 3 ( B ) 5 4 ( C ) 3 5 ( D ) 3 4
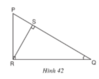
b) Trong hình 42, sin Q bằng:
( A ) PR RS ( B ) PR QR ( C ) PS SR ( D ) SR QR
c) Trong hình 43, cos 30o bằng:
( A ) 2 a 3 ( B ) a 3 ( C ) 3 2 ( D ) 2 3 a 2

Trong các điều kiện sau, câu nào xác định được một véctơ duy nhất?A. Hai điểm phân biệt. B. Hướng của một véctơ.C. Độ dài một véctơ. D. Hướng và độ dài.Câu 2. Mệnh đề nào sau đây là sai?A. a a ≠ ⇔ ≠ 0 0 B. Cho ba điểm A , B , C phân biệt thẳng hàng CA, CBcùng hướng khi và chỉ khi C nằmngoài đoạn AB .C. a, bcùng phương với cthì a, bcùng phương.D. AB AC AC + .Câu 3. Cho ba điểm A , B , C phân biệt thẳng hàng. Câu nào sau đây đúng?A. Nếu B là trung điểm của AC thì AB CB B. Nếu điểm B nằm giữa A...
Đọc tiếp
Trong các điều kiện sau, câu nào xác định được một véctơ duy nhất?
A. Hai điểm phân biệt. B. Hướng của một véctơ.
C. Độ dài một véctơ. D. Hướng và độ dài.
Câu 2. Mệnh đề nào sau đây là sai?
A. a a ≠ ⇔ ≠ 0 0
B. Cho ba điểm A , B , C phân biệt thẳng hàng CA
, CB
cùng hướng khi và chỉ khi C nằm
ngoài đoạn AB .
C. a
, b
cùng phương với c
thì a
, b
cùng phương.
D. AB AC AC + =
.
Câu 3. Cho ba điểm A , B , C phân biệt thẳng hàng. Câu nào sau đây đúng?
A. Nếu B là trung điểm của AC thì AB CB =
B. Nếu điểm B nằm giữa A và C thì BC
, BA
ngược hướng.
C. Nếu AB AB >
thì B nằm trên đoạn AC .
D. CA AB CA AB + = +
.
Câu 4. Mệnh đề nào sau đây là sai?
A. AB AC B C = ⇒ ≡
.
B. Với mọi điểm A , B , C bất kì ta luôn có: AB BC AC + =
.
C. BA BC + = 0
khi và chỉ khi B là trung điểm AC .
D. Tứ giác ABCD là hình bình hành khi và chỉ khi AB CD =
.
Câu 5. Cho tam giác ABC có trực tâm H và nội tiếp trong đường tròn tâm O . B′ là điểm đối xứng
của B qua O . Mệnh đề nào sau đây là sai?
A. AH
, B C′
cùng phương. B. CH
, B A′
cùng phương.
C. AHCB′ là hình bình hành. D. HB HA HC = +
.
Câu 6. Cho tam giác ABC có trọng tâm G , M là trung điểm của BC và O là điểm bất kì. Mệnh đề
nào sau đây là sai?
A. MB MC + = 0
. B. OB OC OM + = 2
.
C. OG OA OB OC = + +
. D. GA GB GC + + = 0
.
Câu 7. Cho ∆ABC có trọng tâm G và điểm M thỏa mãn 2 3 0 MA MB MC + + =
thì GM
bằng:
A. 1
6
BC
. B. 1
6
CA
. C. 1
6
AB
. D. 1
3
BC
.
Câu 8. Cho tam giác ABC câu nào sau đây là đúng?
A. AB AC BC − =
. B. AB CA BC + + = 0
.
C. AC BA CB + =
. D. AB AC BC + >
.
Câu 9. Cho tam giác ABC cân tại đỉnh A . Mệnh đề nào sau đây sai?
A. AB AC =
. B. AB AC BC − =
. C. BC AB AB + =
. D. AB AC =
.
Câu 10. Cho tam giác ABC đều cạnh a . Khi đó AB AC +
bằng:
A. a 3 . B. 3
2
a
. C. 2a . D. 2 3 a .
Cho tam giác ABC vuông tại A, BC = 2AC. So sánh sin B; cos B, khẳng định nào sau đây đúng?
a, sin B < cos B
b, sin B > cos B
c, sin B ≥ cos B
d, sin B = cos B
Qua điểm C nằm ngoài đường tròn (O), vẽ tiếp tuyến CD với đường tròn (O) (D là tiếp điểm). Đường thẳng CO cắt đường tròn tại 2 điểm A và B (A nằm giữa C va B). Kẻ dây DE vuông góc với AB tại H
a, C/m: CED là tam giác cân
b, C/m: OECD là tứ giác nội tiếp
c, C/m: hệ thức AC.BH=AH.BC
Cho các biểu thức A, B, C mà A, B, C 0, khẳng định nào sau đây là đúng? A.
A
BC
AB
C
B
B.
A
B
-
AB
C
BC
C.
A
BC
ABC...
Đọc tiếp
Cho các biểu thức A, B, C mà A, B, C > 0, khẳng định nào sau đây là đúng?
A. A BC = AB C B
B. A B = - AB C BC
C. A BC = ABC BC
D. A BC = ABC BC
Bài 1: Cho (O;R) và điểm A nằm ngoài (O) sao cho OA3R. Từ A vẽ 2 tiếp tuyến AB; AC với (O)a) CMR: Tứ giác OBAC nội tiếpb) CMR: OA ⊥ BCc) Từ B vẽ đường thẳng // AC cắt (O) tại D; AD cắt (O) tại E. Tính AD.AE theo Rd) Tia BE cắt AC tại F. CMR: F là trung điểm ACBài 2: Cho ΔABC nhọn nội tiếp (O); hai điểm B;C cố định. Điểm A di chuyển trên cung lớn BC. Gọi H là hình chiếu của A xuống BC. Gọi M;N lần lượt là hình chiếu của B;C đến đường kính ADa) C/m các điểm A;B;H;M cùng thuộc một đường trònb) C/m...
Đọc tiếp
Bài 1: Cho (O;R) và điểm A nằm ngoài (O) sao cho OA=3R. Từ A vẽ 2 tiếp tuyến AB; AC với (O)
a) CMR: Tứ giác OBAC nội tiếp
b) CMR: OA ⊥ BC
c) Từ B vẽ đường thẳng // AC cắt (O) tại D; AD cắt (O) tại E. Tính AD.AE theo R
d) Tia BE cắt AC tại F. CMR: F là trung điểm AC
Bài 2: Cho ΔABC nhọn nội tiếp (O); hai điểm B;C cố định. Điểm A di chuyển trên cung lớn BC. Gọi H là hình chiếu của A xuống BC. Gọi M;N lần lượt là hình chiếu của B;C đến đường kính AD
a) C/m các điểm A;B;H;M cùng thuộc một đường tròn
b) C/m ΔHMN ∽ ΔABC
c) Gọi I;E lần lượt là trung điểm BC và AB. C/m IE là trung trực của HM
Cho tam giác vuông ABC tại A có tan C = \(\sqrt{3}\). Kết quả nào sau đây là đúng
a. cot B = \(\sqrt{3}\)
b. cot B = 0,8
c. cot C = 1
d. cos B = \(\sqrt{3}\)