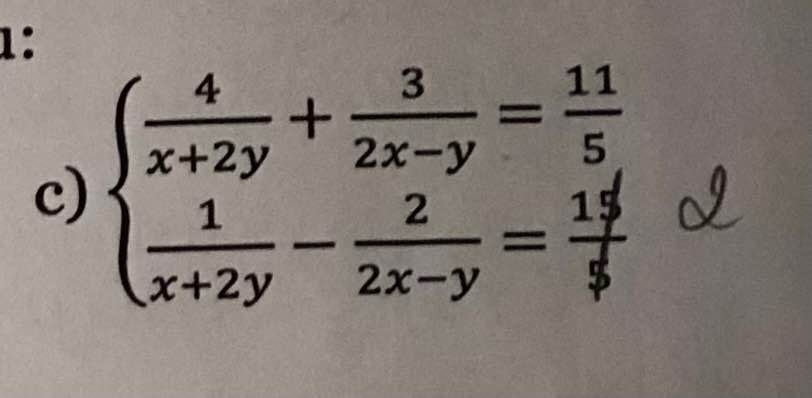ĐKXĐ: x<>-2y; x<>y/2
\(\left\{{}\begin{matrix}\dfrac{4}{x+2y}+\dfrac{3}{2x-y}=\dfrac{11}{5}\\\dfrac{1}{x+2y}-\dfrac{2}{2x-y}=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{4}{x+2y}+\dfrac{3}{2x-y}=\dfrac{11}{5}\\\dfrac{4}{x+2y}-\dfrac{8}{2x-y}=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{4}{x+2y}+\dfrac{3}{2x-y}-\dfrac{4}{x+2y}+\dfrac{8}{2x-y}=\dfrac{11}{5}-8\\\dfrac{1}{x+2y}-\dfrac{2}{2x-y}=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{11}{2x-y}=\dfrac{11}{5}-\dfrac{40}{5}=-\dfrac{29}{5}\\\dfrac{1}{x+2y}=2+\dfrac{2}{2x-y}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x-y=-\dfrac{55}{29}\\\dfrac{1}{x+2y}=2+2:\dfrac{-55}{29}=2+2\cdot\dfrac{-29}{55}=\dfrac{52}{55}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=2x+\dfrac{55}{29}\\x+2y=\dfrac{55}{52}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2x+\dfrac{55}{29}\\x+2\left(2x+\dfrac{55}{29}\right)=\dfrac{55}{52}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=2x+\dfrac{55}{29}\\5x+\dfrac{110}{29}=\dfrac{55}{52}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{11}{52}-\dfrac{22}{29}=-\dfrac{825}{1508}\\y=2\cdot\dfrac{-825}{1508}+\dfrac{55}{29}=\dfrac{605}{754}\end{matrix}\right.\)(nhận)