Chọn A.
Phương pháp:
Đồ thị hàm số lẻ có tâm đối xứng, đồ thị hàm số chẵn có trục đối xứng.
Cách giải:
Quan sát các đáp án ta thấy: Hàm bậc ba là hàm lẻ và có tâm đối xứng nên A đúng.
Các đáp án B, C, D đều là các hàm chẵn nên có trục đối xứng.
Cho hàm số y = x − 1 x − 3 . Xét các mệnh đề sau:
(1) Hàm số nghịch biến trên D = ℝ \ 3
(2) Đồ thị hàm số có một tiệm cận đứng là x=1, tiệm cận ngang là y=3.
(3) Hàm số đã cho không có cực trị
(4) Đồ thị hàm số nhận giao điểm I(3;1) của hai đường tiệm cận làm tâm đối xứng.
Chọn các mệnh đề đúng ?
A. (1), (3), (4)
B. (3), (4)
C. (2), (3), (4)
D. (1), (4)
Cho hàm số y = 7 x 2 có đồ thị (C). Hàm số nào sau đây có đồ thị đối xứng với (C) qua đường thẳng có phương trình y=x
A. y = log 7 x 2
B. y = log 7 x 2
C. y = 1 2 log 7 x
D. y = log 7 x
Đối xứng qua đường thẳng y = x của đồ thị hàm số y = 5 x 2 là đồ thị nào trong các đồ thị có phương trình sau đây?
A. y = log 5 x
B. y = log 5 x 2
C. y = log 5 x
D. y = 1 2 log 5 x
Cho a là một số thực dương khác 1. Có bao nhiêu mệnh đề đúng trong các mệnh đề sau:
1. Hàm số y= l o g a x có tập xác định là D= ( 0 ; + ∞ ) .
2. Hàm số y= l o g a x là hàm đơn điệu trên khoảng ( 0 ; + ∞ ) .
3. Đồ thị hàm số y= l o g a x và đồ thị hàm số y = a x đối xứng nhau qua đường thẳng y= x.
4. Đồ thị hàm số y= l o g a x nhận Ox là một tiệm cận
A. 4
B. 1
C. 3
D. 2
Biết đồ thị (C) ở hình bên là đồ thị hàm số y = a x a > 0 , a ≠ 1 . Gọi (C’) là đường đối xứng với (C) qua đường thẳng y=x
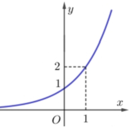
Hỏi (C’) là đồ thị của hàm số nào dưới đây?
A. y = log 1 2 x .
B. y = 2 x .
C. y = 1 2 x .
D. y = log 2 x .
Cho hàm số y = log 2018 1 x có đồ thị C 2 và hàm số y=f(x) có đồ thị C 2 . Biết C 1 và C 2 đối xứng nhau qua gốc tọa độ. Hỏi hàm số y = f x nghịch biến trên khoảng nào sau đây?
A. (-∞;-1)
B. (-1;0).
C. (0;1).
D. (1;+∞)
Cho hàm số y = x − 2 x + 1 . Xét các phát biểu sau đây
+) Đồ thị hàm số nhận điểm I − 1 ; 1 làm tâm đối xứng.
+) Hàm số đồng biến trên tập ℝ \ − 1 .
+) Giao điểm của đồ thị với trục hoành là điểm A 0 ; − 2
+) Tiệm cận đứng là y = 1 và tiệm cận ngang là x = − 1
Trong các phát biểu trên, có bao nhiêu phát biểu đúng?
A. 1
B. 3
C. 2
D. 4
Biết hàm số y=f(x) có đồ thị đối xứng với đồ thị hàm số y = 3 x qua đường thẳng x=-1. Chọn khẳng định đúng trong các khẳng định sau?
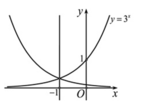
A. f ( x ) = 1 3 . 3 x
B. f ( x ) = 1 9 . 3 x
C. f ( x ) = 1 3 x - 1 2
D. f ( x ) = - 2 + 1 3 x
Cho hàm số y=f(x)=x^3+ax^2+bx+4 có đồ thị (C) như hình vẽ. Hỏi (C) là đồ thị của hàm số y=f(x) nào?
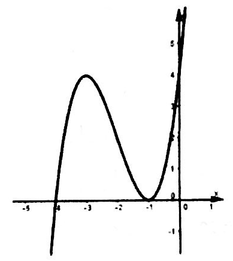
A. y = f ( x ) = x 3 - 3 x 2 + 4
B. y = f ( x ) = x 3 + 6 x 2 + 9 x + 4
C. y = f ( x ) = x 3 + 3 x 2 + 4
D. y = f ( x ) = x 3 - 6 x 2 + 9 x + 4
Tâm đối xứng của đồ thị hàm số y = 1 + 4 x 1 + x là
A. I(4;-1)
B. I(-1;1)
C. I(4;1)
D. I(-1;4)
