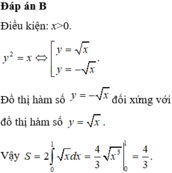Các câu hỏi tương tự
Diện tích hình phẳng giới hạn bởi đường cong
y
2
x
và đường thẳng x1 bằng S là A.
S
2
3
B.
S
4
3
C.
S
1
6
D.
1
3
Đọc tiếp
Diện tích hình phẳng giới hạn bởi đường cong y 2 = x và đường thẳng x=1 bằng S là
A. S = 2 3
B. S = 4 3
C. S = 1 6
D. 1 3
Biết diện tích hình phẳng giới hạn bởi đường cong y=f(x),y=0,x=0,x=2a bằng S. Diện tích hình phẳng giới hạn bởi đường cong y=f(2x), trục hoành Ox và hai đường thẳng x=0,x=a bằng
A. S/4.
B. 4S.
C. 2S.
D. S/2.
Cho hình phẳng (H) giới hạn bởi đường cong có phương trình
y
x
2
-
4
x
+
3
và đường thẳng
y
x
+
3
(phần đô đậm trong hình vẽ). Tính diện tích S của hình phẳng (H). A.
S
47
2
B.
S
39
2...
Đọc tiếp
Cho hình phẳng (H) giới hạn bởi đường cong có phương trình y = x 2 - 4 x + 3 và đường thẳng y = x + 3 (phần đô đậm trong hình vẽ). Tính diện tích S của hình phẳng (H).
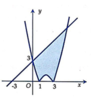
A. S = 47 2
B. S = 39 2
C. S = 169 6
D. S = 109 6
Cho hàm số yf(x) liên tuc trên R và thỏa mãn f(0)0f(-1) Gọi S là diện tích hình phẳng giới hạn bởi các đường
y
f
x
,
y
0
,
x
−
1
v
à
x
1.
Xét các mênh đề sau
1.
S
∫
−
1...
Đọc tiếp
Cho hàm số y=f(x) liên tuc trên R và thỏa mãn f(0)<0<f(-1) Gọi S là diện tích hình phẳng giới hạn bởi các đường y = f x , y = 0 , x = − 1 v à x = 1. Xét các mênh đề sau
1. S = ∫ − 1 0 f x d x + ∫ 0 1 f x d x 2. S = ∫ − 1 1 f x d x 3. S = ∫ − 1 1 f x d x 4. S = ∫ − 1 1 f x d x
Số mệnh đề đúng là
A. 2
B. 1
C. 3
D. 4
Tính diện tích S của hình phẳng giới hạn bởi đường parabol
y
x
3
-
3
x
+
2
và đường thẳng yx-1. A.
S
3
4
B. S 2 C.
S
37
14
D.
S
799
300
Đọc tiếp
Tính diện tích S của hình phẳng giới hạn bởi đường parabol y = x 3 - 3 x + 2 và đường thẳng y=x-1.
A. S = 3 4
B. S = 2
C. S = 37 14
D. S = 799 300
Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số
y
f
x
, trục hoành, đường thẳng x a, x b( như hình bên). Biết
∫
a
c
f
x
d
x
−
2
v
à
∫
c
b
f
x
d
x
5
. Hỏi S bằng ba...
Đọc tiếp
Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f x , trục hoành, đường thẳng x = a, x = b( như hình bên). Biết ∫ a c f x d x = − 2 v à ∫ c b f x d x = 5 . Hỏi S bằng bao nhiêu?
A. 7
B. 5
C. 2
D. 3
Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số
y
x
2
+
2
x
+
1
trục hoành và hai đường thẳng x -1;x3 A. S64/3. B. S56/3. C. S37/3. D. S21.
Đọc tiếp
Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số y = x 2 + 2 x + 1 trục hoành và hai đường thẳng x= -1;x=3
A. S=64/3.
B. S=56/3.
C. S=37/3.
D. S=21.
Gọi S là diện tích của hình phẳng giới hạn bởi đồ thị (C) của hàm số
y
x
4
+
x
2
, trục hoành, trục tung và đường thẳng
x
1
. Biết
S
a
5
+
b
,
a
,
b
∈
ℚ
. Tín...
Đọc tiếp
Gọi S là diện tích của hình phẳng giới hạn bởi đồ thị (C) của hàm số y = x 4 + x 2 , trục hoành, trục tung và đường thẳng x = 1 . Biết S = a 5 + b , a , b ∈ ℚ . Tính a + b
A. a + b = - 1
B. a + b = 1 2
C. a + b = 1 3
D. a + b = 13 3
Gọi S là diện tích hình phẳng (H) giới hạn bởi các đường
y
f
(
x
)
, trục hoành và hai đường thẳng
x
-
1
;
x
2
(như hình vẽ bên). Đặt
a...
Đọc tiếp
Gọi S là diện tích hình phẳng (H) giới hạn bởi các đường y = f ( x ) , trục hoành và hai đường thẳng x = - 1 ; x = 2 (như hình vẽ bên). Đặt a = ∫ - 1 0 f x d x , b = ∫ 0 2 f x d x . Mệnh đề nào sau đây đúng ?
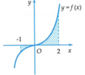
A. S = b - a
B. S = b + a
C. S = a - b
D. S = - b - a