Các câu hỏi tương tự
Diện tích hình phẳng được giới hạn bởi đường cong y = x 2 và đường thẳng y = 2 x + 3 , trục hoành trong miền x ≥ 0 bằng
A. 12
B. 32 3
C. 9
D. 5 3
Biết diện tích hình phẳng giới hạn bởi đường cong y=f(x),y=0,x=0,x=2a bằng S. Diện tích hình phẳng giới hạn bởi đường cong y=f(2x), trục hoành Ox và hai đường thẳng x=0,x=a bằng
A. S/4.
B. 4S.
C. 2S.
D. S/2.
Tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số
y
2
x
-
1
2
trục hoành, đường thẳng
x
2
và đường thẳng
x
3
A. 3 B. 2 C. 1 D. 4
Đọc tiếp
Tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số y = 2 x - 1 2 trục hoành, đường thẳng x = 2 và đường thẳng x = 3
A. 3
B. 2
C. 1
D. 4
Cho (H) là hình phẳng giới hạn bởi đường cong
y
x
, trục hoành và đường thẳng y2-x (phần tô đậm trong hình vẽ bên). Diện tích của (H) bằng A.
4
2
-
1
3
B.
7
6
C.
8
2
+
3...
Đọc tiếp
Cho (H) là hình phẳng giới hạn bởi đường cong y = x , trục hoành và đường thẳng y=2-x (phần tô đậm trong hình vẽ bên). Diện tích của (H) bằng
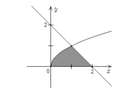
A. 4 2 - 1 3
B. 7 6
C. 8 2 + 3 6
D. 5 6
Cho hình phẳng D giới hạn bởi đường cong
y
2
-
sinx
, trục hoành và các đường thẳng x0,
x
π
2
. Khối tròn xoay tạo thành D quay quanh trục hoành có thể tích V bằng: A.
π
-
1
.
B.
π
2
-
1
.
C....
Đọc tiếp
Cho hình phẳng D giới hạn bởi đường cong y = 2 - sinx , trục hoành và các đường thẳng x=0, x = π 2 . Khối tròn xoay tạo thành D quay quanh trục hoành có thể tích V bằng:
A. π - 1 .
B. π 2 - 1 .
C. π ( π - 1 ) .
D. π 2 + 1 .
Diện tích hình phẳng giới hạn bởi đường cong yf(x), trục hoành và hai đường thẳng x0; x1 là A.
π
∫
0
1
f
2
x
d
x
B.
∫
0
1
f
2
x
d
x
B.
∫
0
1
f
x...
Đọc tiếp
Diện tích hình phẳng giới hạn bởi đường cong y=f(x), trục hoành và hai đường thẳng x=0; x=1 là
A. π ∫ 0 1 f 2 x d x
B. ∫ 0 1 f 2 x d x
B. ∫ 0 1 f x d x
D. ∫ 0 1 f x d x
Miền hình phẳng trong hình vẽ được giới hạn bởi đường cong
y
x
2
+
2
m
x
+
m
2
+
1
, trục hoành, trục tung và đường thẳng x 2. Biết
m
m
0
thì diện tích hình phẳng đó đạt giá trị nhỏ nhất. Giá trị
m
0
gần giá trị nào nhất trong các giá trị sa...
Đọc tiếp
Miền hình phẳng trong hình vẽ được giới hạn bởi đường cong y = x 2 + 2 m x + m 2 + 1 , trục hoành, trục tung và đường thẳng x = 2. Biết m = m 0 thì diện tích hình phẳng đó đạt giá trị nhỏ nhất. Giá trị m 0 gần giá trị nào nhất trong các giá trị sau?
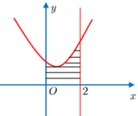
A. 0.
B. 1.
C. 4.
D. -3.
Diện tích hình phẳng giới hạn bởi đường cong
y
a
x
a
0
, trục hoành và đường thẳng
x
a
bằng
k
a
2
(
k
∈
ℝ
)
. Tính giá trị của tham số k. A.
k
6
5
B.
k...
Đọc tiếp
Diện tích hình phẳng giới hạn bởi đường cong y = a x a > 0 , trục hoành và đường thẳng x = a bằng k a 2 ( k ∈ ℝ ) . Tính giá trị của tham số k.
A. k = 6 5
B. k = 4 3
C. k = 2 3
D. k = 3 2
Diện tích hình phẳng giới hạn bởi đường cong
y
ax
,
a
0
, trục hoành và đường thẳng
x
a
bằng
ka
2
,
k
∈
ℝ
. Tính giá trị của tham số k. A.
k
6
5
B.
k...
Đọc tiếp
Diện tích hình phẳng giới hạn bởi đường cong y = ax , a > 0 , trục hoành và đường thẳng x = a bằng ka 2 , k ∈ ℝ . Tính giá trị của tham số k.
A. k = 6 5
B. k = 3 2
C. k = 2 3
D. k = 4 3




