Đáp án C.
y = x3 + 3x2 + 2 suy ra y’ = 3x2 + 6x; y’’ = 6x + 6
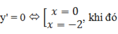
![]()
Vậy điểm cực đại của đồ thị hàm số là (-2;6).
Đáp án C.
y = x3 + 3x2 + 2 suy ra y’ = 3x2 + 6x; y’’ = 6x + 6
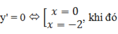
![]()
Vậy điểm cực đại của đồ thị hàm số là (-2;6).
Cho hàm số y = x 3 - 3 x 2 + 2 . Đồ thị hàm số có điểm cực đại là
A. (2;-2)
B. (0;-2)
C. (0;2)
D. (2;2)
Tìm điểm cực đại của đồ thị hàm số y = x 3 - 3 x 2 + 2
A. (2;-2)
B. (2;0)
C. (-2;2)
D. (0;2)
Tọa độ điểm cực đại của đồ thị hàm số y = x 3 - 3 x 2 là
A. 1 ; 3
B. 0 ; 0
C. 0 ; 2
D. 1 ; 2
Tọa độ điểm cực đại của đồ thị hàm số y = x3 – 3x2 + 4 là:
A. (2;4)
B. (2;0)
C. (0;-4)
D. (0;4)
Tìm các giá trị của tham số m để đồ thị hàm số: y = x 3 - 3 x 2 - m x + 2 có điểm cực đại và điểm cực tiểu cách đều đường thẳng có phương trình: y = x - 1 ( d )
A. m = 0
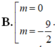
C. m = 2
D. m = - 9 2
Cho hàm số y = (m + 2)x3 + 3x2 + mx - 5, m là tham số. Tìm các giá trị của m để các điểm cực đại, cực tiểu của đồ thị hàm số đã cho có hoành độ là các số dương
A. ![]()
B. 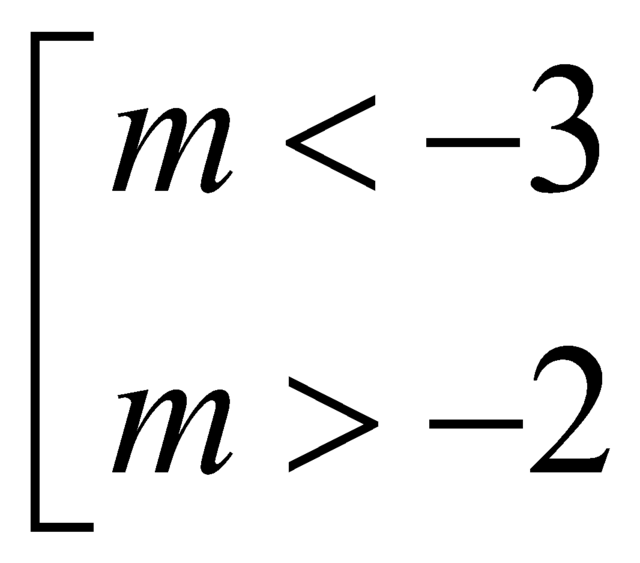
C. ![]()
D. ![]()
Tìm tọa độ điểm cực đại của đồ thị hàm số y = x 3 - 3 x 2 + 3
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số y = x 3 - 3 x 2 + 9 có đồ thị là (C). Điểm cực tiểu của đồ thị (C) là
A. M(0;9)
B. M(2;5)
C. M(5;2)
D. M(9;0)
Cho hàm số y = x 3 - 3 x 2 + m x - m + 1 có đồ thị (C) và điểm A(0;2). Gọi S là tập hợp tất cả các giá trị nguyên của m để có ít nhất 2 tiếp tuyến của đồ thị (C) đi qua A . Tìm số phần tử của S.
![]()
![]()
![]()
![]()